欢迎访问喜蛋文章网
你的位置：首页 > 经典文章 > 文章正文

光速飞行的奥特曼能否永生？（狭义相对论）

时间: 2021-04-12 12:50:04 | 作者：Obliviate | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 110次

光速飞行的奥特曼能否永生？（狭义相对论）

那一天，当他把神光棒交到我的手上的时候，我变成了一道光。

成为奥特曼之后的我拥有了一系列超强的能力。其中有一项重要的能力就是可以接近光速飞行。曾经作为普通人的我从未体验过这种速度，当接近光速时会有什么变化呢？听说到达光速时间会变慢，我是否就得到了永生呢？

为了说明这个问题，就需要向各位科普一下狭义相对论。

首先我们提出一个最基本的概念，叫作“参考系”。

这可以说是狭义相对论中最为重要的一个概念，一切的描述都是基于参考系的，在不同的参考系中可能会有完全不同的结论。比如在地面参考系中子弹正在高速运动，而在飞行员参考系中这可能只是一个悬浮在空中的小东西。因此在作为一个大前提，我们必须要说明“参考系”。

其次，还有一个重要概念是“事件”。所谓“事件”其实和我们平时生活中理解的事件基本是同一个东西，大到火箭发射，小到你在食堂大喊一声“干饭啦！”，所有生物或非生物的行为都可以被称为“事件”

在我们的世界中不断地在发生着各种各样的“事件”。而对于一个事件，忽略掉其本身可能存在的狗血性等无关性质，最基本的两个属性便是“位置”和“时间”。我们该如何描述它们呢？

在描述这两个物理量之前先来说明一下定量描述的重要性。事实上我们会发现在生活语境中大多数描述都是定性描述。比如说一个人长的好不好看啊，这个饭香不香啊等等。定性描述通常不精确，且具有一定的主观性，甚至结论会随着时间改变而颠倒（这就是著名的“真香定律”）。

而定量描述则往往更加准确，且具有客观性。这一点在口红色号的区别上体现的就非常明显。（ps：下面一段为吐槽向内容，不是重点，大家选择阅读就行，创意主要来源于毕导某一期对口红色号的分析，视频链接在文末，有这方面需求的朋友可以前往学习）

（那是在一个月黑风高的晚上，我熟练地掏出手机，在知乎上快乐地摸鱼，突然刷到一篇关于口红色号的推送（作为一个牡丹直男，为什么要给我推这种东西 ）。怀着对新知识的好奇与渴求，我点开了这篇文章。在我看完那篇文章的时候，我开始严重怀疑我是一个色盲。而更为重要的是，这些颜色的名称具有很大的歧义，比如说“酒红色”，到底是哪一个牌子的葡萄酒呢。还有一种居然叫“斩男色”，看的我背后一阵发凉，莫非是斩了男人之后流的血的颜色（我问了某大帅哥，其理解更是有趣——“斩杀男同的涩图”）。之后经过百度，才知道是这是传说中一款唇膏的颜色，风靡万千少女，据说涂上这个颜色的唇膏可以斩获所有直男的心。（也许这个世界上并没有什么斩男色，用的美女多了，也就有了斩男色）。

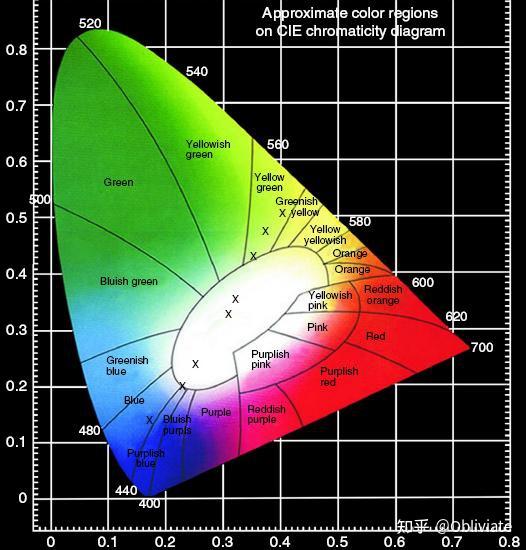
总之这种定性的描述方法具有很大的不便性。为了更加精准的描述这些口红的色号，我们不妨利用毕导提供的CIE色度图的方法对口红的颜色进行定量的描述。当女朋友让你买一支斩男色的口红时，你也许感到困惑，而当她让你买一支CIE色度图上（0.61，0.26）的口红时，是不是突然就变的思路清晰，目标明确了很多

。你甚至可以定制一款CIE色度图上（0.13,0.14）的口红送给女朋友，是不是显得更加浪漫了啊（狗头超级加倍）。总之讲了这么多主要还是为了说明定量描述的重要性。）

接下来，进入正题，如何准确的描述“位置”和“时间”。

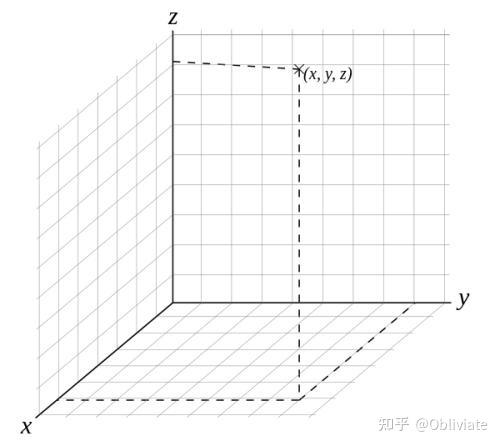
首先是“位置”。为了描述一个事件发生的位置，我们当然不可以用“远啊”“近啊”这种模糊的说法来描述。因此，我们引入小学二年级就学过的“直角坐标系”来描述，确定一个原点和坐标架的放置方向，我们就可以精确的读出在一个空间内的任何一个点的坐标（x,y,z)，那么我们也就得到了这个点的精准的位置了。

直角坐标系

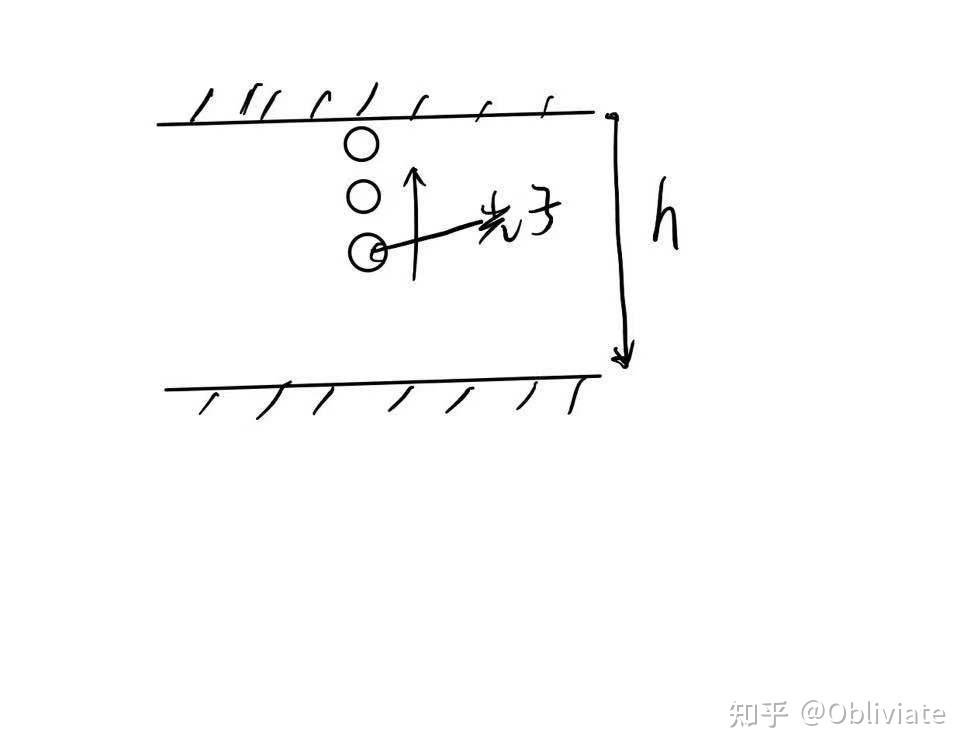
接下来是“时间”。本质上我们就是想要得到一个固定周期的东西，别的时间长度只要加倍就行了。如果采用最原始的单摆来计时间就非常的不靠谱了，因为各种各样的原因会影响单摆的周期（详情请看高中物理选修3-4），于是我们采用光子钟，原理在于光速恒定不变，给定确定的距离h，那么光子运动的每一个周期都是确定的，这样我们就得到了一个绝对准确的时钟。这时我们只要规定某一个时刻为时间原点，在这之前发生的事件的时刻为负，在这之后为正。

光子钟

到现在为止我们已经为“参考系”装备了准确测量“位置”和“时间”的工具，那么我们就可以准确的得到一个参考系中的所有事件发生的位置和时间了。（ps：我们认为一个参考系中的位置和时间是瞬间得到的，而不是说一定要通过某种信号传递到我们所在的位置我们才可以得到这些信息，即我们是站在全知视角来看的，这一点非常重要的）

但事实上参考系有无数多个，不同的参考系发生着相对运动，运动可以非常复杂，可以是变速运动或是曲线运动，但我们只讨论其中最简单的匀速直线运动。

接下来便是狭义相对论里最重要的一个问题了，对于同一个事件，在不同参考系中它发生的位置和时间有什么关系。在我们经典的时空观里，不同的参考系中时间都是相同的，不会因为你在运动你的一天就变长了。而位置的变换关系是我们从小学就接触的相遇和追及问题中的简单变换关系（x’=x-vt,y’=y,z’=z.t’=t)。但这真的对吗？在低速情况下是对的，但接近光速时这种变换就不成立了，这里直接提出正确的变换方式，是以下的洛伦兹变换。（我们可以看到低速下两者是接近的）

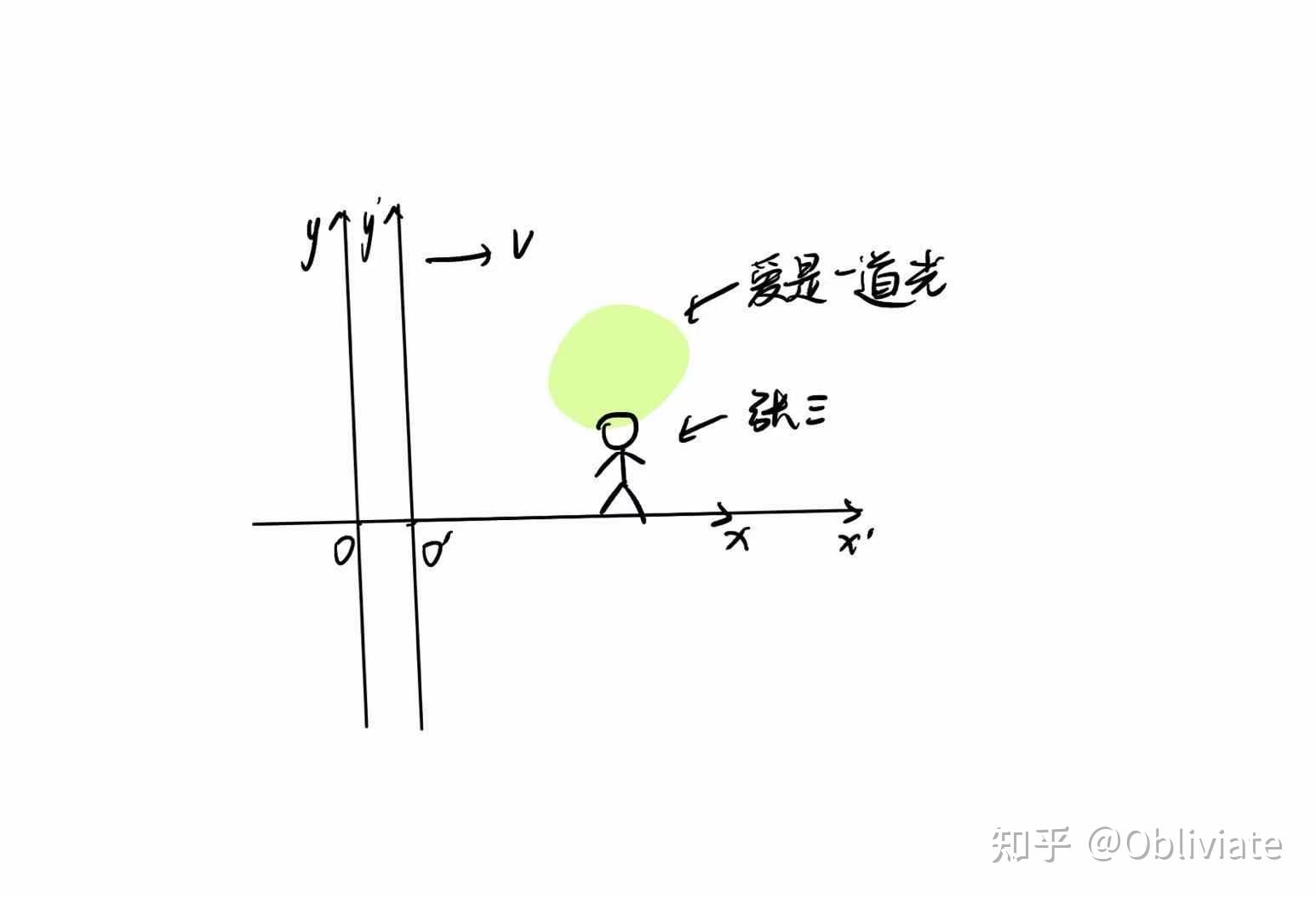
举个栗子。

在t=0的时刻S和S'参考系的坐标架完全重合，S’是相对S参考系向右以u=0.6c（c是光速）运动的参考系。假设在S系中，我们发现在t=1s，x=1光秒（1光秒是光走一秒的距离）处张三头顶发出一道闪亮的绿光，那么请问在S’中什么时候（t’)什么位置(x’)张三头顶发光了呢？

那么到现在为止我们已经会套公式来解决问题了。那么这个公式是怎么来的呢？这是基于相对论的两个基本假设推出的，一个是相对性原理，另一个是光速不变原理，基于这两个原理我们就可以得到这样的公式（证明过程较为复杂，其中也具有很深刻的物理意义，感兴趣的朋友可以自己去查找相关教科书阅读）。

到现在为止总结一下，我们现在与平时的认知的唯一区别就是不同参考系里的位置和时间不是想当然的变换，而是需要套公式来算了。

接下来介绍在狭义相对论中的两个重要的效应——“尺缩”和“钟慢”效应。我们直接用洛伦兹变换来解释它们。

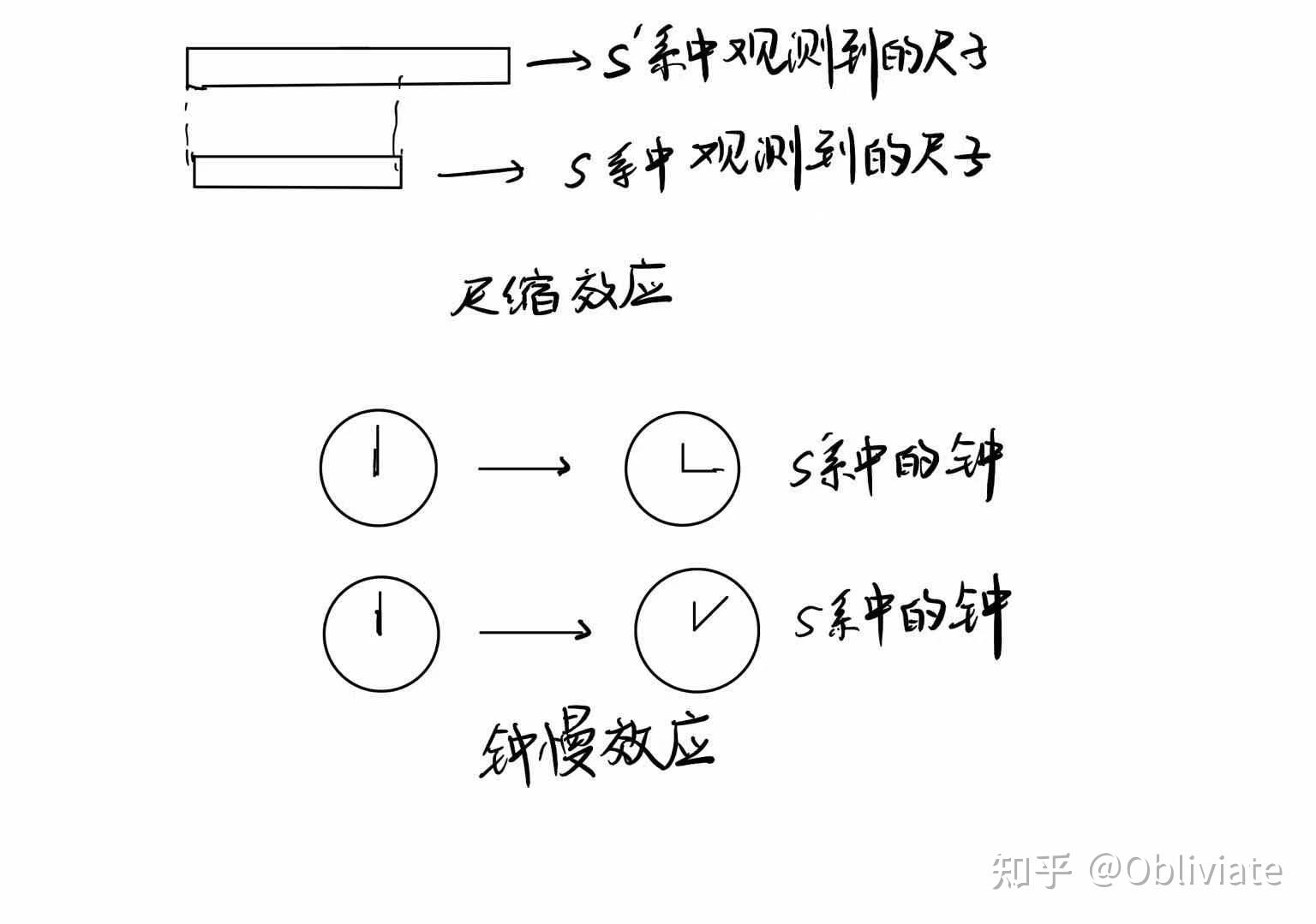
所谓“尺缩”，就是在一个参考系看来另一个相对运动的参考系中事物的长度会收缩。

在说明这个原因之前，首先我们应该知道怎么测量长度。比如对于一把尺子，我们想要测量它的长度，我们需要在同一时间记录下它的起始位置和终点位置，之后作差即可。这是小学生都能想明白的道理。

我们注意到刚才所说的办法中提到了重要的两个概念“时间”“位置”。这两个概念是依赖于“参考系”的，因此“长度”这个概念同样依赖于参考系，也就是说在不同参考系中尺子的长度也会不同，那么到底是变长了还是变短了，又变化了多少呢？这里我们用洛伦兹变换来说明。

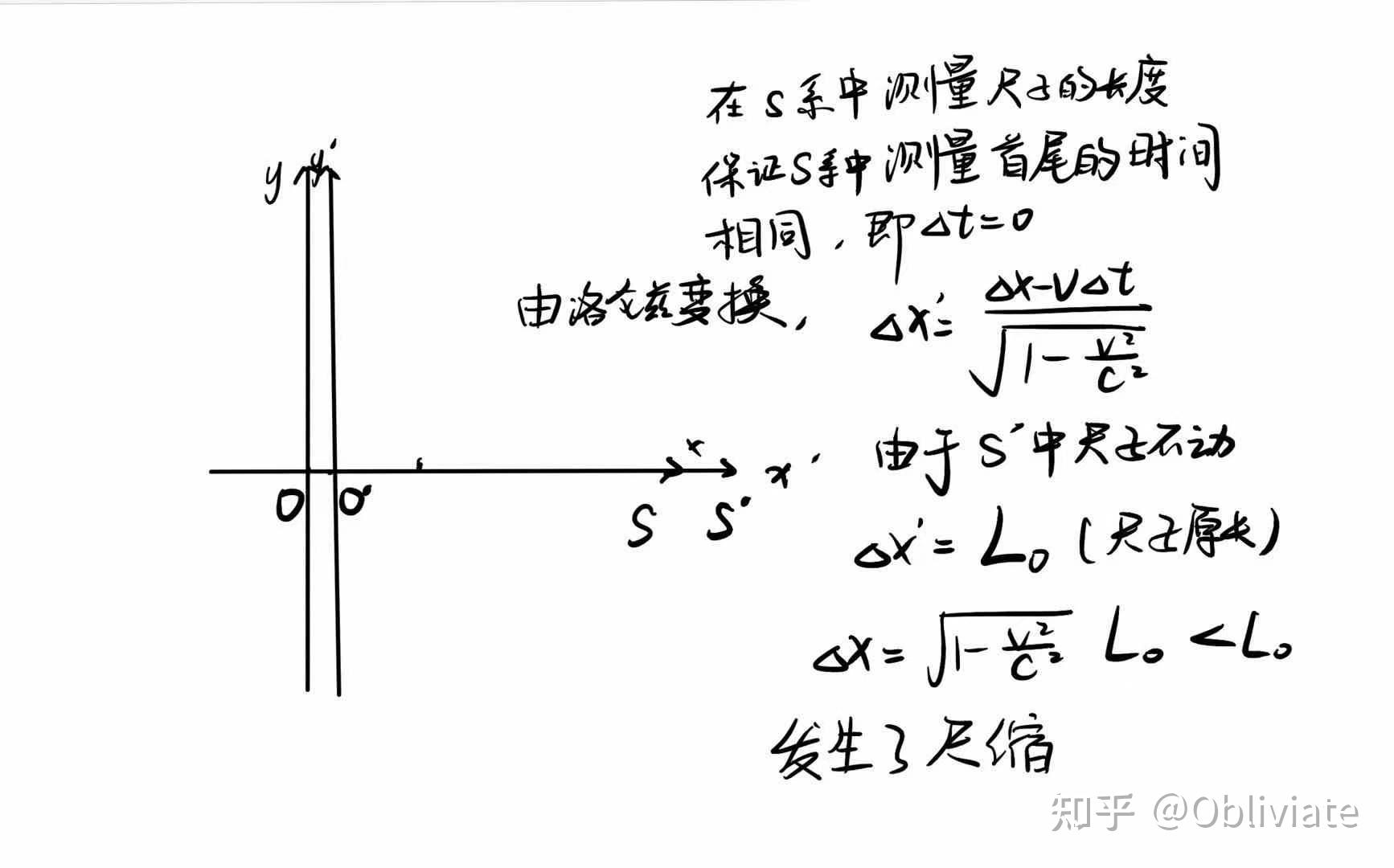
（利用尺缩效应，我们可以得到这样一个结论，只要跑得够快，在别人眼里你就会收缩，就能瘦成一道闪电。） 所谓钟慢，就是说在一个参考系中看来另一个相对运动的参考系中的固定位置的时钟走得变慢了。这是为什么呢，我们可以直接用洛伦兹变换来解释。

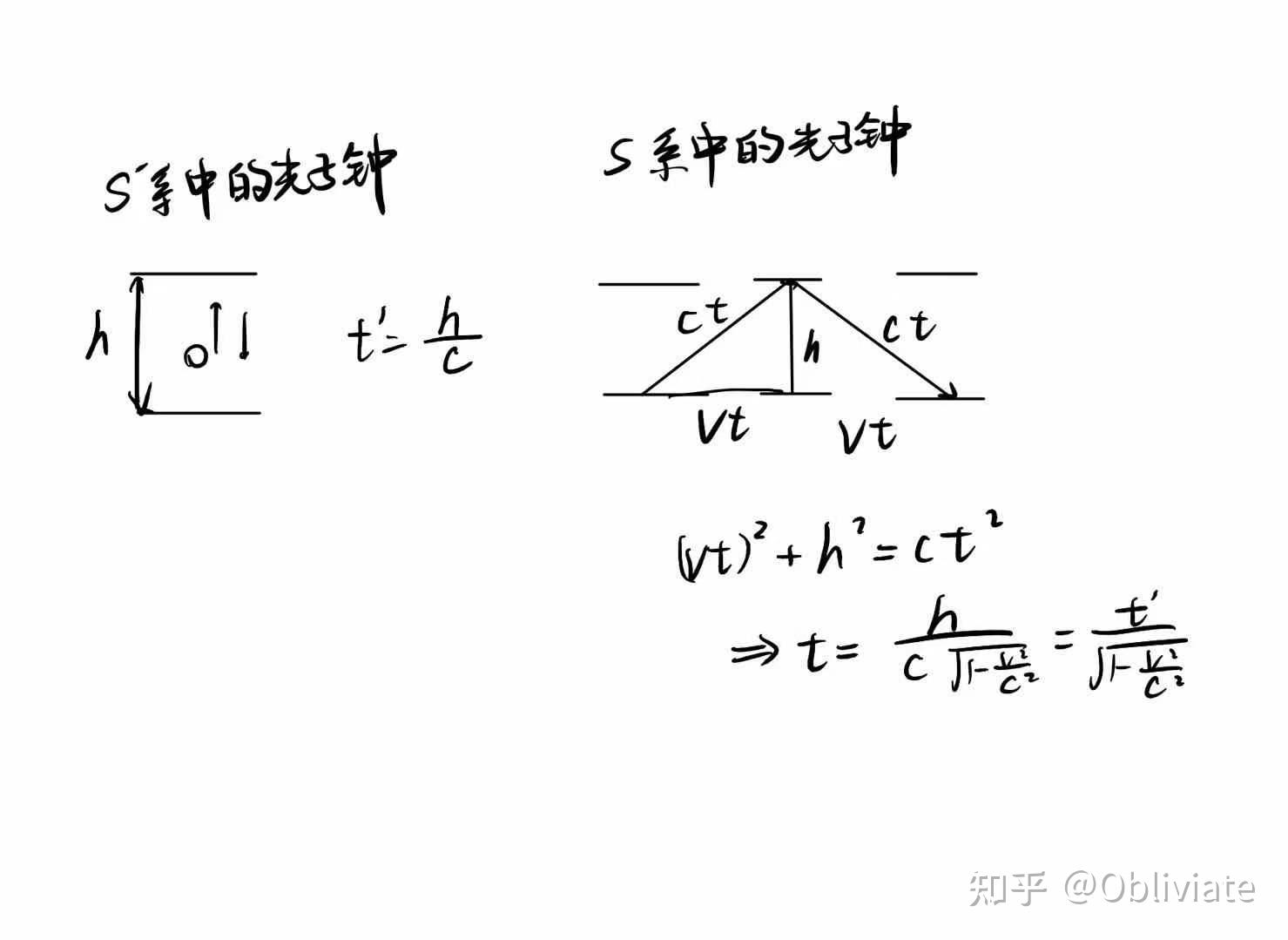
这里在补充一种有趣的证明钟慢的办法。之前我们提到了用光子钟来计时的办法，我们这边同样引入光子钟。

解释一下，根据光子钟的原理，时间等于光子路程除以光速，由基本假设光速不变，变化的只有光子的行进路程，这一部分的变化来源于光子钟跟随着S'的运动，在S系中看来就有横向运动了

（有些大聪明知道了钟慢效应之后就开始妄想各种骚操作，比如说什么在考试的时候摇头到接近光速就可以比别的同学多思考很多时间啥的）

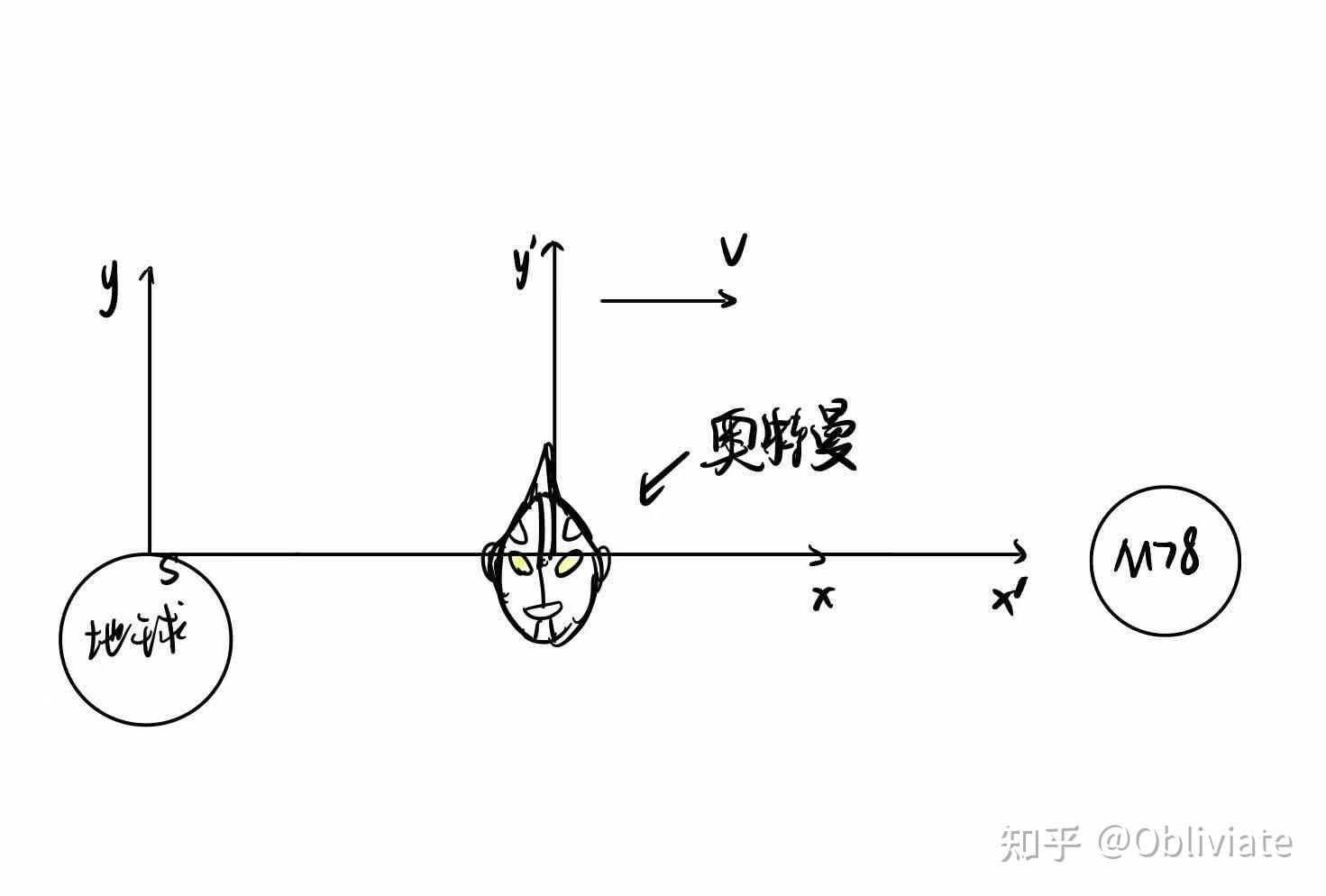
那么我们回来解释最开始的问题，光速飞行的奥特曼到底能不能永生？

这个问题本质上就是钟慢效应。根据钟慢效应，的确在地球参考系中看来，光速飞行的奥特曼参考系中时间变慢了。可是我们反过来看，根据相对性原理，在奥特曼看来，地球上的人也是永生的。事实上，我们站在奥特曼参考系中，时间在正常的流逝，奥特曼仍然在正常的生活，也就是说在主观感觉上接近光速飞行的生活不会有任何变化，只是在地球参考系中所看到的场景不一样而已。

所以说，所谓的永生只是在地球参考系上看来如此，而奥特曼并不会有这样的感觉。那么如果你是想得到主观上的无限生存时间，靠快速运动是做不到的，但想让别人觉得你永生了，那确实如此。

可是有些同学仍然感到困惑，经过比较，年龄计算上来看两者数据确实不同啊，这是为什么呢？事实上，这种比较本身就没啥意义，因为我们所在的观测参考系都不同，参考系不同，比较的维度也已经不同了，有意义的比较的前提是在同一个参考系。所以对于时间是否变长的问题的纠结主要来自我们常规经验的束缚，是对此反常现象的困惑，但这个问题本身就是没有意义的，用数据说话是最准确的。

最后，总结一下，狭义相对论告诉我们最重要的一个道理就是，描述一切事件的前提就是确定参考系，不说明参考系,就啥也不是,理解了这个道理也就差不多入门了狭义相对论的时空观。

这时你是否顿悟了，原来狭义相对论里包含着这样深刻的人生哲理，你看到的永远只能是在你的参考系中的世界，对于别人的世界，你只能通过某种换算来推理。而客观的位置和时间至少还可以通过洛伦兹变换来得到，但切换了参考系，别人的心理就难以推算了。也许，这就是爱情吧。

全文部分素材来源于网络，如有侵权请联系我删除。（其中毕导口红色号那期视频的传送门：https://www.bilibili.com/video/BV1NK411M7kS

from=search&seid=9472493680281021059）

文章标题: 光速飞行的奥特曼能否永生？（狭义相对论）
文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/101739.html
文章标签：狭义相对论  科学  物理科普
Top