欢迎访问喜蛋文章网
你的位置：首页 > 经典文章 > 文章正文

【油果酱】-每周分享-BPHO真题-质心公式的来源以及应用

时间: 2021-10-16 10:41:56 | 作者：油果酱 | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 101次

【油果酱】-每周分享-BPHO真题-质心公式的来源以及应用

昨天一位同学问了一个关于质心的问题。今天稍微聊聊质心计算方法的来源和应用。

题目来自BPhO_Round_1_2021_sec_1，的第(i）小问

A square metal plate of uniform density has dimensions 3R × 3R. Its centre is the centre of a Cartesian coordinate system，with axes parallel to the edges of the plate. A complete circular region, radius R, is removed from the plate. Determine the position of the centre of gravity of the remaining square plate when the centre of the circular hole is at (i) (x, 0) and (ii) (x, y).

这是一道典型的质心问题。

按照惯例先翻译。

一块正方形，密度均匀的金属板，尺寸为3R×3R. 其中心为平面直角坐标系的原点，各条边与坐标轴平行。同时从这个金属板中切走一块半径为R的圆形片。请确定剩下的金属板的质心所在的位置，若切走的圆片的圆心在(i) (x, 0) and (ii) (x, y)

在BPHO阶段需要掌握的质心公式为

x_{cm}=frac{Sigma m_i cdot x_i}{Sigma m_i}

这个题目如果正面去求解，有些复杂。因为如下图所示，剩余部分质量的图形为不规则图形。

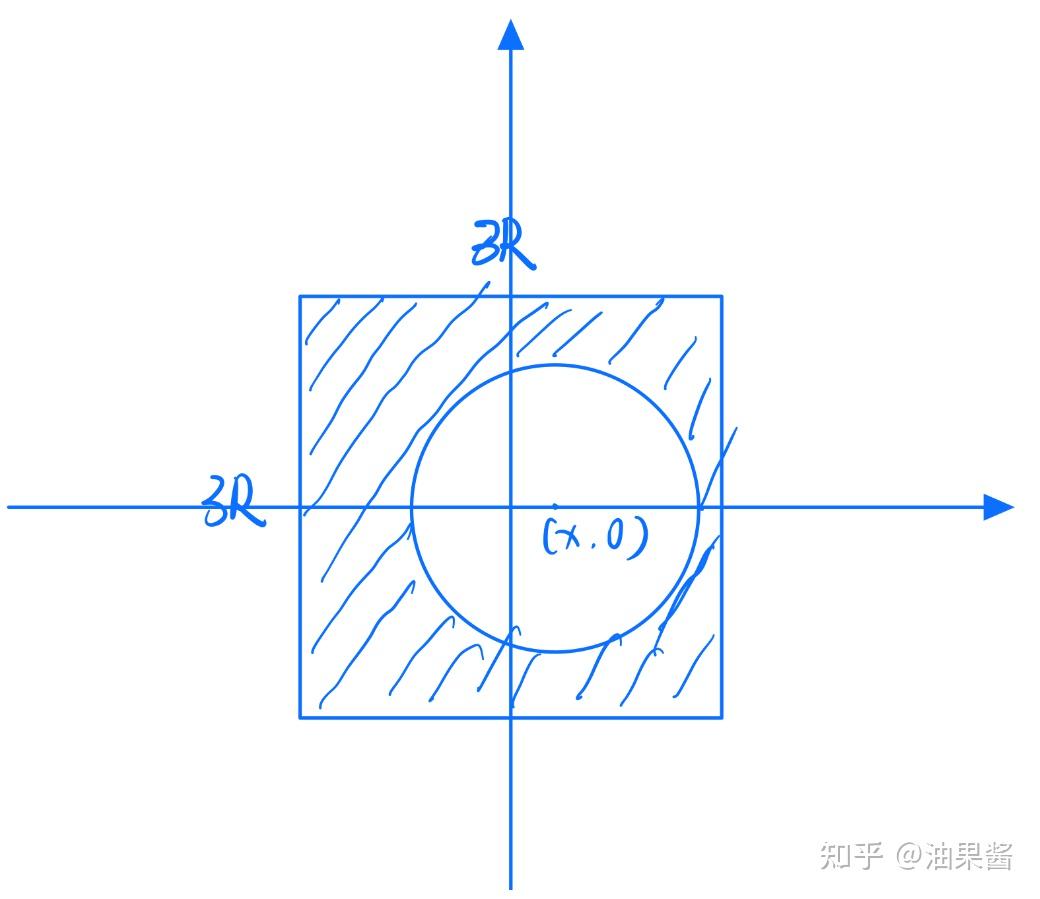
所以我们反过来思考，假设上图中阴影部分的质量为m1，圆形部分质量为m2. 那么这两个质量的组合就是原来的完整正方形，同时组合之后的系统质心坐标落于原点上。

假设m1的质心坐标为 (x_1,y_1) ,m2的质心坐标为 (x_2,y_2) 。

同时由于金属板的密度是均匀的，假设其面密度为 sigma

那么 m_2=sigmapi R^2 , m_1=sigma(9R^2-pi R^2)

我们可以列出方程组 begin{equation*} begin{cases} x_{cm}=frac{sigma (9R^2-pi R^2)cdot x_1+sigmapi R^2cdot x_2}{sigma 9R^2} y_{cm}=frac{sigma (9R^2-pi R^2)cdot y_1+sigmapi R^2cdot y_2}{sigma 9R^2} end{cases} end{equation*}

其中质心的坐标为（0， 0），同时圆的圆心坐标就是m2的质心为 x_2=x, y_2=y。

上述方程化简为 begin{equation*} begin{cases} 0=(9-pi)cdot x_1+pi cdot x 0= (9-pi )cdot y_1+pi cdot y end{cases} end{equation*}

解得剩余部分质量的质心坐标为 begin{equation*} begin{cases} x_1=frac{pi x}{pi-9} y_1=frac{pi y}{pi-9} end{cases} end{equation*}

其实两个小问是一个问题。

---分割线---

这里再聊聊质心公式的来源

系统的动量 textbf{P}=Sigma textbf{p}_i

适当选取一个参考系 K^{'} 使得系统的总动量变为0. 这样的参考系，称为系统的零动量系或者动量中心系(center-of-momentum system).

按照伽利略变换，在K'参考系中的动量为( m=Sigma m_i )

P'=Sigma m_i v_i'=Sigma m_i(v_i-V)=Sigma m_iv_i-mV

变形得到 V=v_c=Sigmafrac{m_iv_i}{m}=frac{P}{m}

使得 P'=0 ，把K'变成动量中心系 K^{CM} ,这里的 v_c 便是质量中心系 K^{CM} 相对于K系得速度。因为 v_i=dr_i/dt ,这里 r_i 是第i个质点得位矢，于是

v_c=Sigmafrac{m_ifrac{dr_i}{dt}}{m}

由于在牛顿力学当中，质量与速度无关，上式可以写成

v_c=frac{d}{dt}(Sigmafrac{m_ir_i}{m})

两边同时对时间积分，可以得到

r_{CM}=frac{Sigma m_ir_i}{Sigma m_i}

这就是我们最终希望得到得质心公式了。

谢谢你看到最后，下面是我目前正在填充的两个专栏。有兴趣的同学不妨点击进去看看。

文章标题: 【油果酱】-每周分享-BPHO真题-质心公式的来源以及应用
文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/126016.html
文章标签：物理科普  高中物理  物理竞赛
Top