你的位置：首页 > 经典文章 > 文章正文

悬链线方程的推导

时间: 2021-07-23 16:27:31 | 作者：遥相辉映的战士 | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 116次

悬链线方程的推导

因为计算过程会出现双曲函数，所以先简单了解一下双曲函数

在数学中，双曲函数是一类与常见的三角函数（也叫圆函数）类似的函数。最基本的双曲函数是双曲正弦函数 sinh 和双曲余弦函数 cosh ，从它们可以导出双曲正切函数 tanh 等，其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数，有反双曲正弦函数 arcsinh ，反双曲余弦函数 arccosh ，反双曲正切函数 arctanh 。

双曲函数的定义和三角函数有如下关系

sinhx=-isinix

coshx=cosix

$tanhx=frac{sinhx}{coshx}=frac{-isinix}{cosix}=-itanix$ 是虚数单位

sinhx 和 tanhx 都是奇函数， sinh(-x)=-sinhx ， tanh(-x)=-tanhx

coshx 是偶函数， cosh(-x)=coshx

双曲正弦和双曲余弦导数关系:(求导方式就是把虚数单位当成常数，其它步骤一样)

(sinhx)'=coshx

(coshx)'=sinhx

双曲函数还可以用指数函数来表示

根据欧拉公式 $e^{ix}=cosx+isinx$

得 $e^{x}=e^{i(-ix)}=cosix-isinix=coshx+sinhx$

$e^{-x}=e^{i(ix)}=cosix+isinix=coshx-sinhx$

即 $sinhx=frac{e^{x}-e^{-x}}{2}$ ， $coshx=frac{e^{x}+e^{-x}}{2}$

接下来看悬链线

悬链线是一根密度均匀的绳子或铁链两端固定在水平杆上，受重力的作用自然下垂后形成的曲线

既然能保持平衡，那这根绳子上一定处处都满足二力平衡。绳子受到重力以及自身张力

假设一条不可伸长的线密度为 rho 的绳子处于重力加速度为的重力场中，取绳子上某一小段受力分析，这小段在轴上的投影是

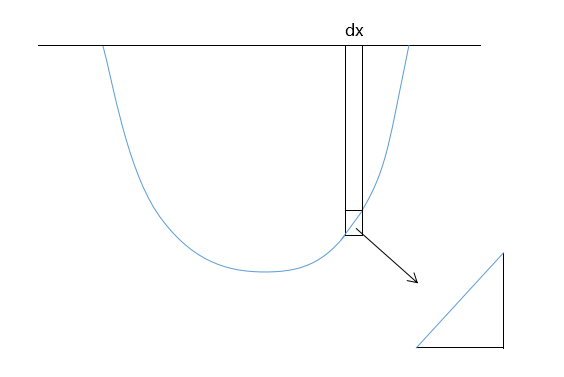
小段绳子和水平面夹角的正切值就是悬链线方程在那一点的导数

可以证明，这段绳子的长度为 $dl=frac{dx}{costheta}=sqrt{1+tan^{2}theta}dx=sqrt{1+y'^{2}}dx$

图为受力分析

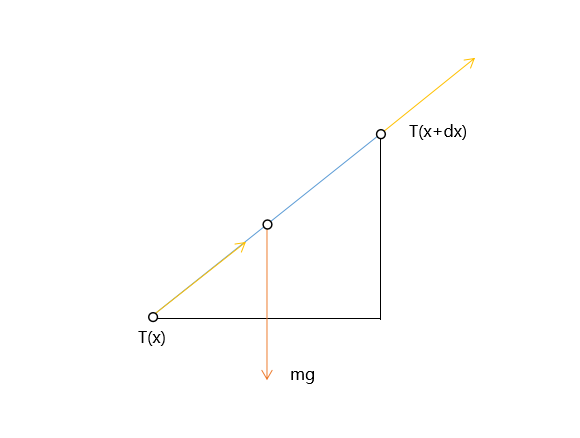
所受重力为 $mg=rho dl=rho gsqrt{1+y'^{2}}dx$ ，受到的它前面那段绳子的拉力为 $T(x+dx)=(T_{x}(x+dx),T_{y}(x+dx))$ ，且 $T_{y}=T_{x}y'$ ，它对后面那段绳子的拉力为 $T(x)=(T_{x}(x),T_{y}(x))$ 。所以这段绳子受到的合力为 $F=T(x+dx)-T(x)+mg=(frac{dT_{x}}{dx}dx，frac{dT_{y}}{dx}dx-rho gsqrt{1+y'^{2}}dx)=(0,0)$

$frac{dT_{x}}{dx}=0$ ，所以 $T_{x}=c$ ，横向的张力是一个定值。又有 $frac{dT_{y}}{dx}=rho gsqrt{1+y'^{2}}$ ，且 $T_{y}=T_{x}y'=cy'$ ，所以 $frac{dT_{x}y'}{dx}=frac{cdy'}{dx}=cy''=rho gsqrt{1+y'^{2}}$

就得到了悬链线的微分方程 $y''=ksqrt{1+y'^{2}}$

分离变量 $y''=frac{dy'}{dx}=ksqrt{1+y'^{2}}$ ， $frac{1}{sqrt{1+y'^{2}}}dy'=kdx$

$int_{}^{}kdx=int_{}^{}frac{1}{sqrt{1+y'^{2}}}dy'$

令 y'=it ，即 dy'=idt ，是虚数单位

$int_{}^{}kdx=kx+c_{1}=int_{}^{}frac{1}{sqrt{1+y'^{2}}}dy'=iint_{}^{}frac{1}{sqrt{1-t^{2}}}dt=iarcsint=iarcsin(-iy')$

所以 $y'=isin(-i(kx+c_{1}))=-isin(i(kx+c_{1}))=sinh(kx+c_{1})$

$y'=sinh(kx+c_{1})$

$y'=frac{dy}{dx}=sinh(kx+c_{1})$ ， $dy=sinh(kx+c_{1})dx$ $int_{}^{}dy=y=int_{}^{}sinh(kx+c_{1})dx=frac{1}{k}cosh(kx+c_{1})+c_{2}$

把 $frac{1}{k}$ 记为，得到悬链线方程 $y=acosh(frac{x}{a}+c_{1})+c_{2}$

可以看出 $c_{1}$ ， $c_{2}$ 和坐标原点的选取有关，如果把悬链线的顶点选在坐标原点(顶点 y'=0 )那么 $c_{1}=0$ ， $c_{2}=-a$ ，悬链线方程为 $y=a(coshfrac{x}{a}-1)$

也可以用指数函数表示 $y=afrac{e^{frac{x}{a}+c_{1}}+e^{-(frac{x}{a}+c_{1})}}{2}+c_{2}$

悬链线的方程和密度 rho 以及重力加速度的大小无关。如果原先定好了铁链的长度是的话可以通过 $l=int_{x_{1}}^{x_{2}}sqrt{1+y'^{2}}dx$ 求出 ( $x_{1}$ , $x_{2}$ 是两个悬挂点的位置)。不过也只能得到 $l=asinh(frac{x_{1}}{a}+c_{1})-asinh(frac{x_{2}}{a}+c_{1})$ 没法用初等函数表示出 a=f(l) 的形式

补充一下

如果这根绳子不是不可伸长的绳子，而是符合胡克定律的弹性绳，而且下垂时每一段小绳子只会在纵向发生形变(其实这种性质更像纵向变形的均匀杆)。

这种绳子只有纵向张力没有横向张力。纵向张力满足 $T=kfrac{dy}{dx}$ ，这种绳子自由下垂形成的曲线是抛物线

证明如下，假设绳子的线密度是 rho ，重力加速度是

绳子的合力 $F=T(x+dx)-T(x)+mg=frac{dT}{dx}dx-rho gdx=0$

得 $frac{dT}{dx}=rho g$ ，即 $frac{dT}{dx}=frac{dkfrac{dy}{dx}}{dx}=kfrac{d^{2y}}{dx^{2}}=ky''=rho g$

这个曲线的微分方程为 $y''=frac{rho g}{k}$

解得 $y=frac{rho g}{2k}x^{2}+c_{1}x+c_{2}$

文章标题: 悬链线方程的推导

文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/116236.html

文章标签：物理科普力学悬链线

[悬链线方程的推导] 相关文章推荐：

2023-08-28 09:00:07怎样认知中国古代的力学知识
2023-05-23 07:00:26量子力学的重要性是什么
2023-03-22 22:00:42应该如何理解热力学第二定律的这两种表述
2023-03-13 09:04:56物理科普的渠道有哪些
2023-03-04 09:02:17为什么熵和系统的热力学概率的自然对数成正比
2023-03-03 15:00:52什么是岩土力学
2023-03-01 10:01:48热气球涉及哪些流体力学的知识
2023-02-13 12:01:20量子力学有多可怕
2023-01-27 12:04:58牛顿力学有什么关键理论
2023-01-12 12:00:20《高等量子力学》主要讲述了什么样的内容

最新经典文章

热门经典文章

Top

全站搜索