【高中】匀变速直线运动-几个重要推论
时间: 2021-08-06 19:27:53 | 作者:文须雀物理大百科 | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 110次
- 2023-08-07 01:01:37高中物理老师总说“化雪天比下雪天冷”,那为什么相比于化雪天更暖和的下雪天雪不会融化呢
- 2023-07-07 14:01:00你觉得高中学习的物理知识中最实用的是什么
- 2023-06-16 22:01:37高中物理社可以安排怎样的狠活或花活
- 2023-03-13 09:04:56物理科普的渠道有哪些
- 2023-01-21 22:01:40高中物理有哪些经典的实验
- 2023-01-02 12:04:32理论物理科普有什么意义
- 2022-12-06 17:59:55高中物理电磁学有哪些考点
- 2022-10-26 21:00:18高二 有哪些关于物理科普类的书啊
- 2022-01-02 03:00:56有哪些好的适合高中和大学的物理科普书籍
- 2021-08-19 20:40:48我出书了! 《什么是高中物理》

重要推论
做匀变速直线运动的物体,在某段时间内中间时刻的瞬时速度等于这段时间内的平均速度.即:即:
即:
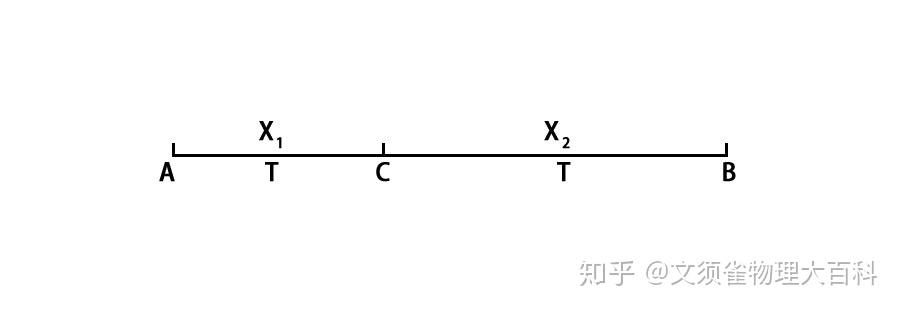
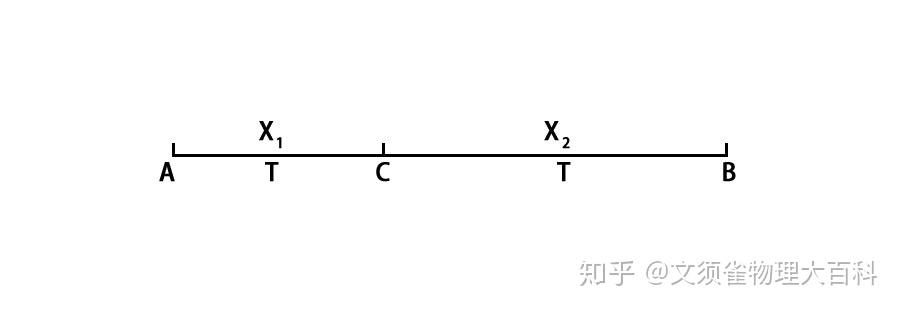
联立以上两式得:.
即得:
即得:
即得:
即得:
即得:
例题
【例】一物体沿斜面顶端由静止开始做匀加速直线运动,最初内的位移为
,最后
内的位移为
,已知
;
,求斜面的总长.
【解析】由题意知,物体做初速度等于零的匀加速直线运动,相等的时间间隔为3s.由题意知,,解得
,
物体做初速度等于零的匀加速直线运动,相等的时间间隔为3s.由于连续相等时间内位移的比为:
.故
,可知
,解得:
.又因为,
,所以斜面的总长:
.【答案】
文章标题: 【高中】匀变速直线运动-几个重要推论
文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/118649.html
[【高中】匀变速直线运动-几个重要推论] 相关文章推荐:
- 最新经典文章
- 热门经典文章
- 热门文章标签
全站搜索