孔明灯究竟能飞多高？

前几天也不知道是什么节日，见到小区里有几个人在放飞孔明灯，大小近半人多高，升起后渐渐飘至高处远处，忽暗忽明，时隐时现，煞是有些神秘。因为天上是神话中神灵居住的地方，又让人觉得孔明灯有几分神灵的气息。只见广场上一对恋人一边放飞一边认真地双手合拢地朝天祷告着，祝我们……。

孔明灯据传为我国古代三国时期诸葛亮所发明，将蜡烛置于纸糊的笼内点燃后即可升空随风飘荡。热气上浮是一种随处可见的日常现象，可是能想到把蜡烛放入纸笼中的人，则属于诸葛亮之类的奇才。

但是孔明灯究竟能飞多高呢，某网站说孔明灯能最高能飞到1万米，本人亦对此问题颇感兴趣，看看能不能根据一些基本的物理知识和数据估算出其飞行高度的范围。

孔明灯的上升的动力来源于灯内外空气之间的密度差，当灯内的蜡烛点燃时，灯内半封闭空间内空气被加热温度升高，而温度高的空气的密度低于温度低的密度，所以灯周围的冷空气将孔明灯向上推动。这一现象人们在日常生活中可以大量见到，例如蜡烛的火焰朝上飘，锅里的蒸汽向上漂浮，海水在日光下蒸腾上升为云等。

但是要想知道孔明灯究竟能飞到多高，则需要一些更具体的数据和计算，本例中则首先需要知道灯内的空气在点燃蜡烛后能升高到多少度？在这个温度下的空气的密度是多少？等等。

据查蜡烛燃烧时火焰的温度约在300~600°C，那么孔明灯空气整体的平均温度肯定不会超过600°C，考虑到热空气会从灯底部的开口不断逸出，灯内空气的平均温度不会太高。又因为灯罩为纸质材料，而纸的燃点范围为130~250°C，所以假定灯内的空气平均温度为200°C，根据气体方程我们知道气体密度与温度成反比，也就是：

①

上式中T1，T2分别大气温度和点燃蜡烛后灯内的温度，ρ1为常温时的空气密度，ρ2为高温时的空气密度，此时T1=273K，T2=200+273=473K，设此时为零度，而零度时大气的密度为1.29kg/m3,代入上式中得：

②

即200°C时灯内的热空气密度为0.7447kg/m3，我们知道空气的密度将随着高度的上升而下降，也就是说当孔明灯上升到空气密度接近0.74kg/m3的高度时，就会失去浮力而下坠，那么这个高度时多少米呢？根据《物理手册》，当高度在10公里以下时空气的密度经验公式如下，其中 =1.225 Th1=283.15K：

③

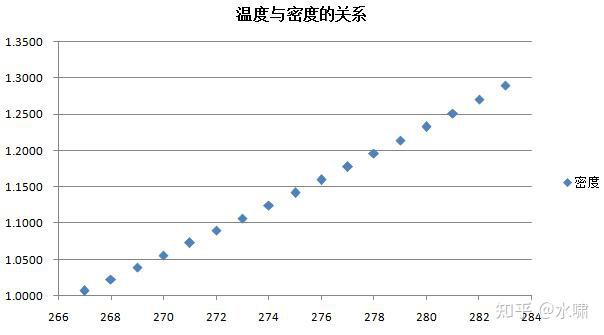
式中的Th1为海平面上的温度，Th2为高空中的温度，而高空中的温度的计算公式如下：

Th2=Th1-0.0065h ④

这里的h为海拔高度。

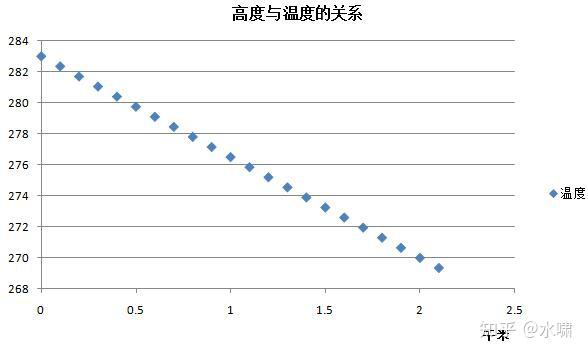
假定h为1万米，则其温度为：

Th2=Th1-0.0065h= Th1-0.0065*10000=283.15-65=218.15K=-55°C

将此温度代入密度计算公式③ 中：

这说明1万米高空的空气密度0.4034 kg/m3已经低于我们刚才计算出的孔明灯内的空气的密度0.7447kg/m3，显然已经不能再产生浮力，也就是说纸质的孔明灯是绝对不可能上升到1万米高空的，那么仅仅考虑温度及密度时孔明灯的上升极限高度是多少呢？根据公式④，高空5000米处的温度为：

Th2=Th1-0.0065h=283.15-0.0065*5000=283.15-32.5=250.65K=-22.5°C

将此温度代入公式③得到5000米高空的密度：

此时的空气密度0.7227kg/m3已经略低于灯内的空气密度0.7445kg/m3,这说明如果仅仅考虑纸质孔明灯的温度上限，即使忽略其自身重量其上升高度将不会超过5000米。

实际上由于孔明灯尚须克服自身的重量，因此其灯内密度必须要比灯外的空气密度还要低，这样才能克服自身重力而浮起，因此实际的上升高度的上限要比这个还要低一些，下面我们根据孔明灯的具体的重量数据进行计算，据淘宝上的某款孔明灯的介绍，其具体的尺寸等数据如下：

灯高h=82cm 灯柱的半径r=22cm，总重量W=60克=0.06kg，蜡块重量Wl=13.7克=0.0137kg，蜡块的燃烧时间ts=5.8分钟=348s。

据以上数据，灯的体积为：

V=πr2*h=3.14*0.22^2*0.82=0.1246（m3）

该体积所能产生的浮力大小为：

而该款灯的总重为0.060kg，克服其重力后仅略有剩余。当灯上升后高处的密度 会

下降而 则没有变化，当灯上升至100米处时，根据公式④：

Th2=Th1-0.0065h=Th1-0.0065*500=283.15-0.65=282.5K

代入高空密度计算公式③中：

此时灯所产生的的浮力大小如下：

Ff（500米）=

=0.059（kg）

该浮力的大小已经小于孔明灯的自重0.06kg了，因此根据此款孔明灯的尺寸大小和所使用的蜡块的大小，其上升高度将不会超过100米。

且慢，因为在上升时蜡块自身燃烧灯的自重会减少，这将会使其上升高度的上限得到提高，因蜡块的重量为13克即0.013kg，蜡块烧尽后灯的重量W2=60-13.7=46.3克=0.0463kg，根据这个重量我们根据上述公式逆算，设蜡块烧尽后所达到的高度处空气密度为

从而求出

再利用式③计算此时对应的高空温度Tx：

把 代入上式：

解上述方程求得上升停止时的高空温度为277.03K

再根据此温度利用式④计算此处的高度：

Th2=Th1-0.0065h 此时Th2=277.03K代入

277.03=283.15-0.0065hx

hx=（283-277.03）/0.0065=918.5(m)

也就是说考虑到蜡块燃烧后重量的减少对上升高度的提升作用后，该款孔明灯的最大上升高度约为919米。

我们还可以根据厂家提供的蜡块燃烧时间5.8分，50秒的预热时间进一步地计算出灯的上升速度v：

v=919/(5.8*60-50)=3.1(米/秒)

这个速度折合时速为11公里/小时属于低速行驶的汽车或人类跑步的速度，该是符合我们观察到的实际上升的速度。我们又知道降落伞的落下时的末端速度为6米/秒，考虑到孔明灯的脆弱的构造，其上升速度应该低于6米/秒是合理的。

综上计算得出的结果是这款孔明灯的上升高度的上限为919米，而其他不同尺寸的孔明灯的上升的上限高度也会尺寸及构造不同而有所不同，但是只要是纸质的孔明灯其上升高度绝对不会超过5000米。

任何计算都是需要经过实际验证才能证明其正确性是小编的一贯的观点，但是在实际上还有另一种方法进行验证，那就是交叉验证法。所谓的交叉验证法就是对同一问题采用不同的方法去计算解答，如果所获得的答案接近或相同，那么通过实际验证的可能性就非常大，反之则不成立的可能性非常大。所以下面采用另一种方式来计算一下孔明灯的上升高度。

设灯的总质量为m，体积为V，灯柱的高度为h，半径为r，灯所受的上升浮力为Ff，地面的空气密度为ρ1，加热后灯内的空气密度为ρ2，根据伟大的阿基米德浮力定律灯所受到的浮力等于灯内气体重量的减少：

Ff=（ρ1-ρ2）*V*g=（ρ1-ρ2）*πr2h*g ⑤

设灯上升时所受到的空气阻力为fa，根据空气动力学当物体在流体中低速运动时，其阻力与运动速度v成正比：

fa=kv ⑥

上式中k为低速运动时阻力系数，取决于物体材质和形状等。

分析孔明灯的运动过程，在上升之初有一段加速运动，之后将处于升力与阻力和重力平衡的状态，在平衡状态下根据牛顿力学：

Ff=mg+kv ⑦

把⑤式代入上式得：

（ρ1-ρ2）*πr2h*g=mg+kv ⑧

观察上式，当孔明灯上升后大气密度（ρ1）密度将逐渐减小，这时灯的上升速度将逐渐下降，当v=0时，

（ρ1-ρ2）*πr2h*g-mg=0 ⑨

整理⑨得：

ρ1πr2h*g=mg+ρ2*πr2h*g

ρ1= +ρ2 ⑩

密度ρ1 为该款孔明灯上升到最大高度时周围大气的密度，也就是之前计算得出的1.1162kg/m3，注意这里m应是蜡烛烧尽后的灯的重量46.3克。分析上式就可以知道孔明灯上升高度的上限与空气阻力系数k无关，所以利用牛顿力学分析所得出的结果与之前用密度差计算时所得出的表达式是相同的，因此两者所得出的孔明灯的上升高度上限也是相同的，用不同的方法得出了相同的结果，这就说明之前的密度差法的计算结果相当可信。

那么如何通过实验验证上述计算结果呢？买来该款孔明灯实际放飞？但是如何才能测得它的上升的实际高度呢？雷达是探测不到的，目测又不准确，在孔明灯上系上根绳子的话将会大大改变系统的重量，最多只能目测到放飞时的上升速度和大致的漂浮时间，这个也与上述计算大致相符合……所以笔者确实无法想出比较靠谱的实际验证的方法，无奈之下只能将其留给更加聪明的读者了。

[孔明灯究竟能飞多高？] 相关文章推荐：

• 2023-10-05 00:01:40历史类的科普与自然科学类科普相比有什么区别
• 2023-03-30 20:01:16哪些植物可以用来制作孔明灯
• 2023-03-19 15:00:15怎么样才能学习自然科学的基础知识
• 2023-03-13 09:04:56物理科普的渠道有哪些
• 2023-03-03 15:00:41如何评价这些动物的特点，真实习性和行为，并且怎样的动物生活习性和行为方式，才能够经得住自然科学的检验
• 2023-03-01 18:02:09国家自然科学奖几年评一次
• 2023-01-02 12:04:32理论物理科普有什么意义
• 2022-10-26 21:00:18高二 有哪些关于物理科普类的书啊
• 2022-10-16 18:00:47古代欧洲有哪些自然科学研究成果
• 2022-05-14 18:00:26为什么自然科学里很多公式符合平方反比定律，为什么指数是 2 不是 3