欢迎访问喜蛋文章网
你的位置：首页 > 经典文章 > 文章正文

The physics behind ski jumping

时间: 2021-04-12 12:47:50 | 作者：HZ2Y | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 100次

The physics behind ski jumping

As we all know, ski jumping is one of the most popular winter sport all over the world. Have you ever try to find out the physics principle behind the sport and try to explain the motion in mathematical way.

Here is a ski jumping model question which is from Canadian Association of Physicists (CAP) 2021 question paper. It is a kind of ski jumping because the path of the ball is similar to the counterparts.

From CAP 2021 question paper

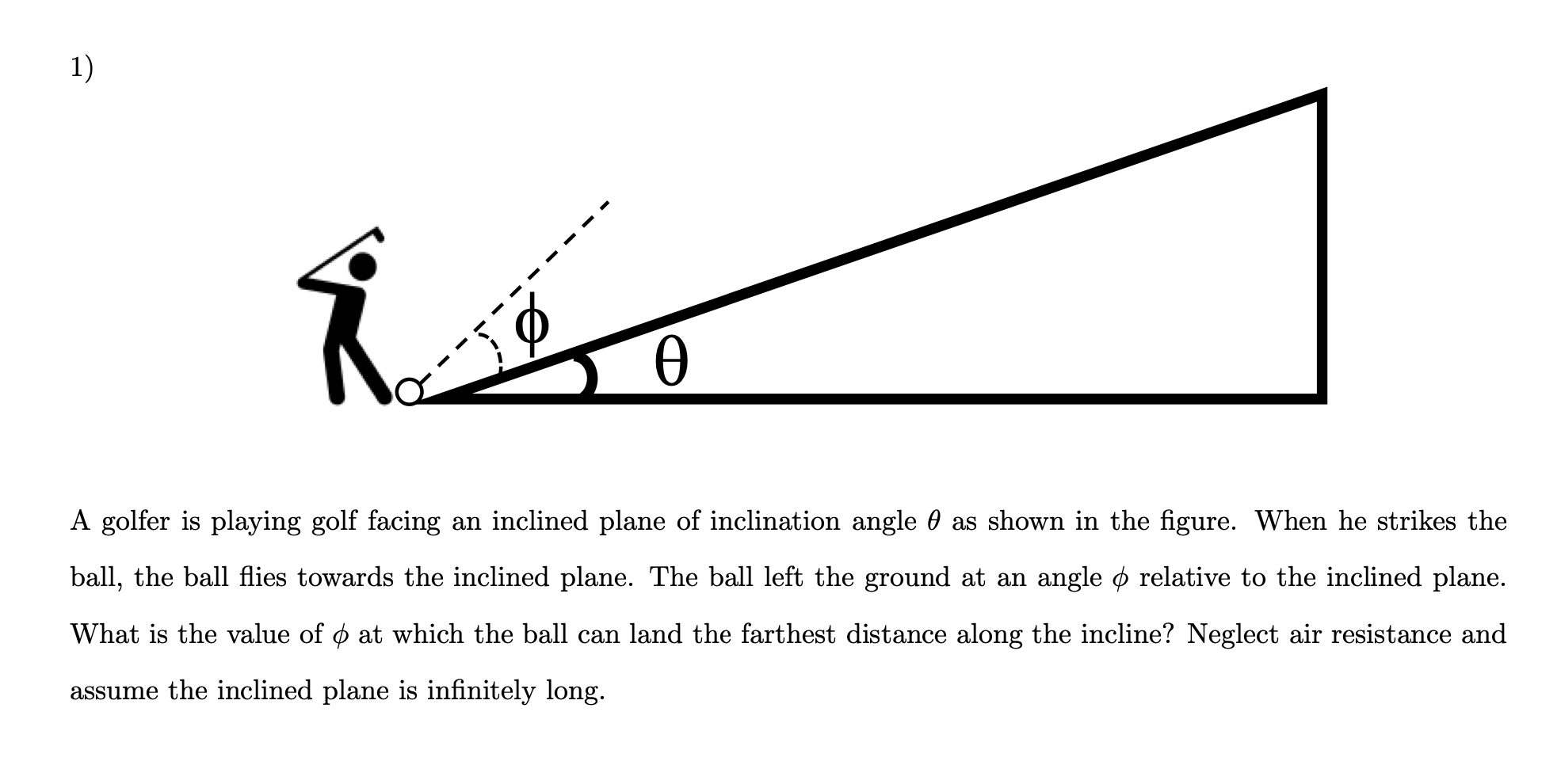
So let’s start with analysis this question. We usually solve this type of question by decompose the velocity into X-axis and Y-axis：

begin{cases}x=Vcdot tcdot cos(phi +theta)y=Vcdot tcdot sin(phi +theta)-frac{1}{2}gcdot t^{2} end{cases}

Then we can get a formula t in terms of x:

t= frac{x}{Vcdot cos(phi +theta)}

The next step is substitute t into y, we can obtain an expressive of y in terms of x:

y=frac{Vcdot x cdot sin(phi +theta)}{V cdot cos(phi +theta)}+frac{x^2 cdot g}{2 cdot g cdot V^{2} cos^{2}(phi + theta)}

We can simplify this expression into:

y =tan(phi + theta)cdot x - x^{2}cdot frac{g}{2V^{2}cdot cos^{2}(phi +theta)}

Since:

y = tan(theta)cdot x

So:

tan(theta)cdot x=tan(phi +theta)cdot x-x^2 cdot frac{g}{2V^2 cos (phi+theta)}

x = frac{2V^2 cos^2 (phi +theta)}{g}cdot [tan(phi +theta)-tan(theta)]

x= frac{V^2}{g}[2tan(phi+theta)cdotcos^2 (phi+theta)-cos^2(phi +theta)cdot tan(theta)]

x= frac{V^2}{g}[2sin(phi+theta)cdotcos (phi+theta)-2cos^2(phi +theta)cdot tan(theta)]

Then we can use double angle formula to simplify it further:

sin(2A)=2sin(A)cdotcos(A)

x=frac{V^2}{g} cdot [sin (2phi +2theta)-2tan(theta)cdot cos^2 (phi +theta)]

So we get x in terms of theta . The next stages involve differentiation question, if you don’t know how to deal with it, you can just skip this stage. It may make you confuse about the following phases. So I will show you the basic differentiation formula we need in this question:

frac{d}{dx}(sinx)=cosx

frac{d}{dx}(cosx)=-sinx

frac{d}{dx}(tanx)=sec^{2}x

frac{d}{dx}[f(x)pm{g(x)}]=frac{d}{dx}[f(x)]pmfrac{d}{dx}[g(x)]

In order to find the maximum of x in terms of theta , so we have to find out the first derivative of the function and let it equal to zero:

frac{dx}{dtheta}=frac{2V^2}{g}cdot cos(2phi +2theta)+frac{4V^2}{g}tan(theta)cdotsin(phi +theta)cdot cos(phi+theta)

frac{dx}{dtheta}=frac{2V^2}{g}cdot cos(2phi +2theta)+frac{4V^2}{g}tan(theta)cdotsin(phi +theta)cdot cos(phi+theta)=0

Then we use double angle formula again to simplify the expression:

frac{dx}{dtheta}=frac{2V^2}{g}[cos(2phi +2theta)+tan(theta)cdot sin(2phi +2theta)]

Let the first derivative equal to zero, since 2 square V over g is constant, so just let the part in the brackets equal to zero:

cos(2phi +2theta)+tan(theta)cdot sin(2phi +2theta)=0

Use trigonometric function transformation:

cos (A)=sin(A)cdot cot(A)

We get:

sin(2phi +2theta)cdot cot(2phi +2theta)+tan(theta)cdot sin(2phi +2theta)=0

sin(2phi+2theta)[cot(2phi+2theta)+tan(theta)]=0

We know that theta is a constant:

begin{cases}sin(2phi+2theta)=0tan(theta)=-cot(2phi+2theta)end{cases}

We can mention that:

tan(theta)=-cot(frac{pi}{2}+theta)

At the end:

cot(frac{pi}{2}+theta)=cot(2phi+2theta)

The answer is:

phi= frac{pi}{4}-frac{theta}{2}

Then we will focus on another problem (real ski jumping question)

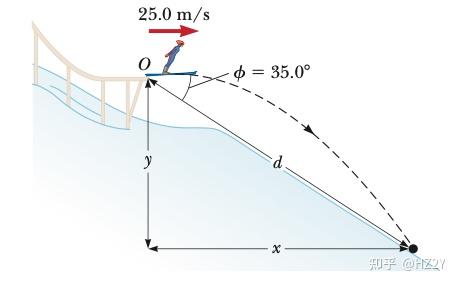
figure from《Physics for Scientists and Engineers with Modern Physics Ed10》
We categorize the problem as one of a particle in projectile motion. As with other projectile motion problems, we use the particle under constant velocity model for the horizontal motion and the particle under constant acceleration model for the vertical motion. From 《Physics for Scientists and Engineers with Modern Physics Ed10》

By first, we find out the coordinates of the jumper as a function of t:

begin{cases}x_f =v_{xi}cdot t=dcdot cos(phi)--(1)y_f=-frac{1}{2}cdot gcdot t^2 =-d cdot sin(phi)--(2)end{cases}

(3)t=frac{dcdot cos(phi)}{v_{xi}}

Then we substitute (3) into (2):

dcdot sin(phi)=frac{g}{2}cdot (frac{dcdot cos(phi)}{v_{xi}})^2

Rightarrow d=frac{2cdot v_{xi}cdot sin(2phi)}{gcdot cos^2(phi)}

The final step is substitute the data into the equation, I won't show you the step but the final answer:

final answer begin{cases}d=109x_f =89.3 y_f =-62.5 end{cases}

Then let us move on a further question:

A skier leaves the ramp of a ski jump with a velocity of v = 10.0 m/s at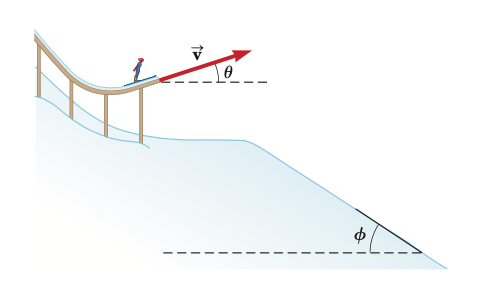 theta = 15degrees above the horizontal as shown in Figure. The slope where she will land is inclined downward at phi = 50 degrees, and air resistance is negligible. Find (a) the distance from the end of the ramp to where the jumper lands and (b) her velocity components just before the landing. (c) Explain how you think the results might be affected if air resistance were included.
figure from《Physics for Scientists and Engineers with Modern Physics Ed10》

begin{cases}x_f =v_{xi}cdot t cdot cos(theta)y_f=v_{xi}cdot sin(theta) cdot t-frac{1}{2}cdot gcdot t^2 end{cases}

t=frac{x_f}{v_{xi}cdot cos(theta)}

substitute t into x_f:

y=frac{x_f cdot v_{xi}cdot sin(theta)}{v_{xi}cdot cos(theta)}-frac{g}{2}cdot frac{x_f^2}{v_{xi}cdot cos^2(theta)}

We can mention that it is a quadratic function, also we can express the slope into a linear equation:

y=-tan (phi)cdot x_f

So we let then equal:

frac{x_f cdot v_{xi}cdot sin(theta)}{v_{xi}cdot cos(theta)}-frac{g}{2}cdot frac{x_f^2}{v_{xi}cdot cos^2(theta)}=-tan (phi)cdot x_f

We can draw the path in this way:

(I plus 40 on each but it won't change anything just make it look nice in the first quadrant)

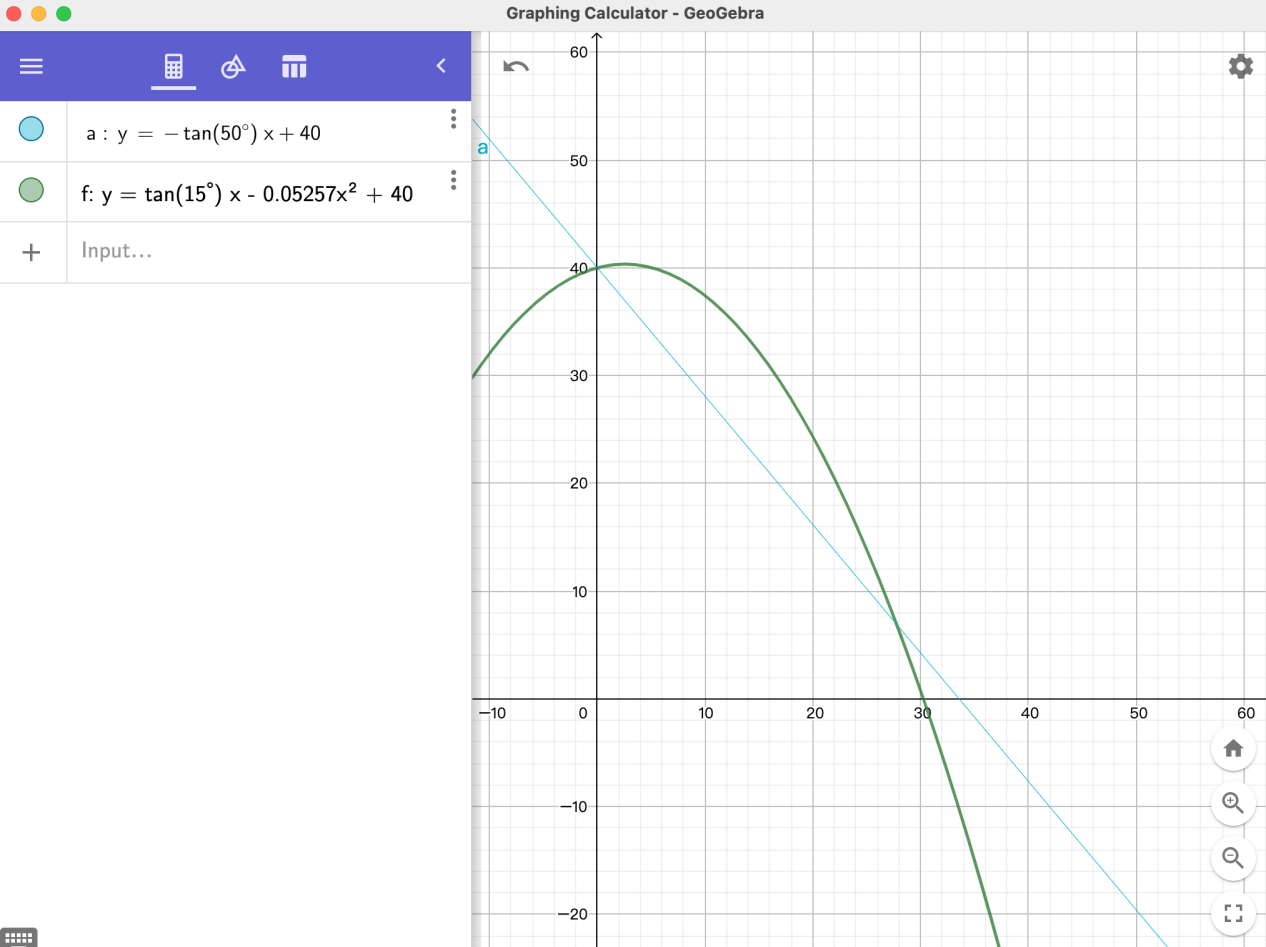
At the end, you will find it not hard to solve the equation, so I will not show you the question. Here is a video which is talking about the same thing in other way, if you're not clear please watch this video.

https://www.youtube.com/watch?v=xOpCP0ZPmWM&t=24s​www.youtube.comhttps://www.youtube.com/watch?v=QT8dYTNeZmM&t=97s​www.youtube.com

In the last, if you have any problem of the article you can ask me anything via private mail.

If you think that it is helpful for me, subscribe me and I will upload more things about physics, thanks!

文章标题: The physics behind ski jumping
文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/101736.html
文章标签：物理科普  高中物理
Top