欢迎访问喜蛋文章网
你的位置：首页 > 读后感 > 文章正文

《推荐系统实践》笔记 第二章 利用用户行为数据

时间: 2021-10-18 09:39:56 | 作者：xaropc | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 113次

《推荐系统实践》笔记 第二章 利用用户行为数据

这是有关项亮《推荐系统实践》的阅读笔记。最近准备进行推荐系统的入门，全英文网课入手有些困难，因此找了以本中文的书先大概了解一下。笔记主要是对书籍的内容分章节进行整理，大体服从原书的结构。因为我还是新手，很多地方还不是很懂，欢迎大家一起讨论。

第二章 利用用户行为数据

在很多情况下，了解用户的兴趣非常困难，因此可以考虑通过挖掘用户的行为数据来获取用户的兴趣。

2.1 用户行为数据简介

用户行为数据在网站上最简单的存在形式就是日志。用户行为主要有两种，显性反馈行为(explicit feedback)与隐性反馈行为(implicit feedback)。显性的如“喜欢”、“不喜欢”以及评分，隐性的主要是用户的页面浏览行为。

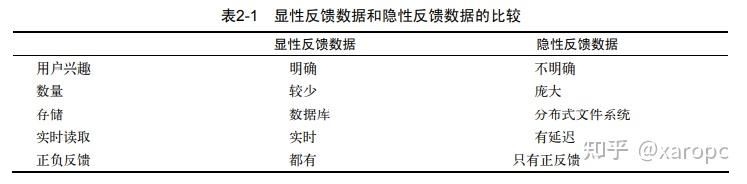
也可以按照反馈的方向分类，包括正反馈与负反馈。简而言之，正反馈就是喜欢，负反馈就是不喜欢。

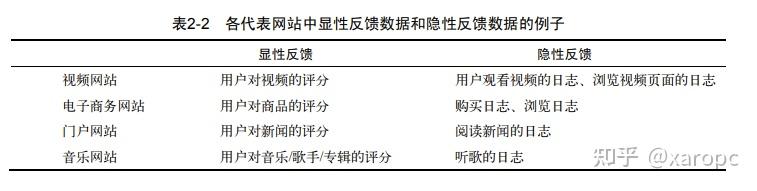
2.2 用户行为分析

2.2.1 用户活跃度与物品流行度的分布

二者满足长尾分布。下图中横坐标为程度，纵坐标为数量。用户的活跃度表示用户产生过行为的物品总数。为了更加直观，对图中的曲线进行了取对数操作。

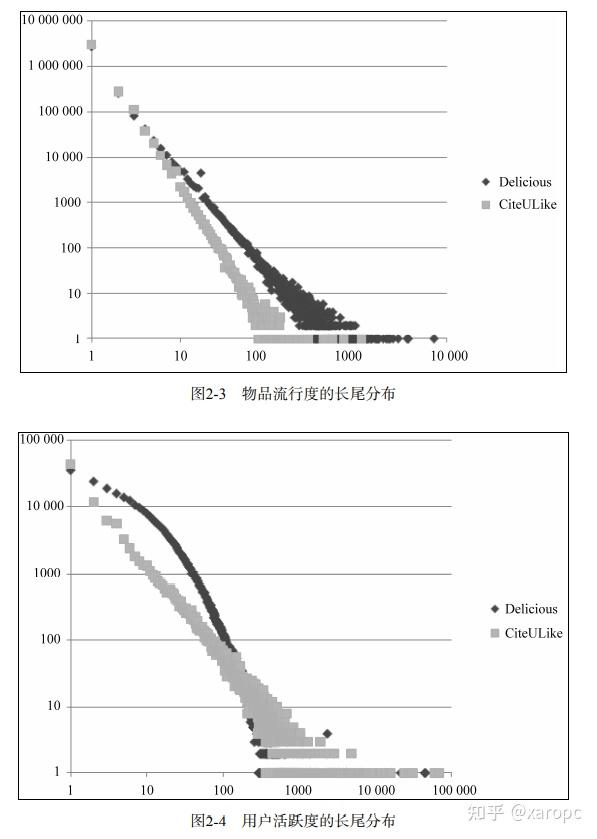
2.2.2 用户活跃度与物品流行度的关系

一般认为，新用户倾向率浏览热门的物品，而老用户会逐渐开始浏览冷门的物品，如下图所示：

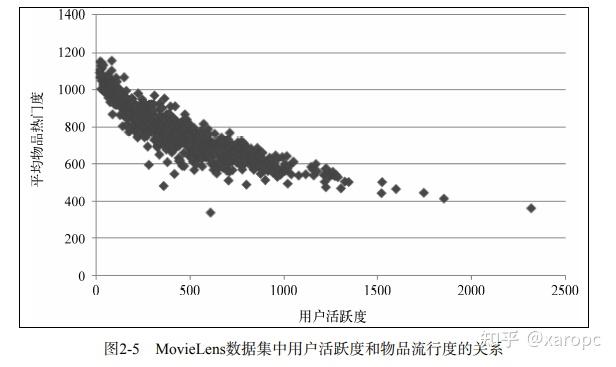
仅仅基于用户行为数据设计的推荐算法一般叫做协同过滤算法，主要有基于邻域的方法(neighborhood-based)、隐语义模型(latent factor model)、基于图的随机游走算法(random walk on graph)等。其中基于邻域的算法最为常用，主要有基于物品、基于用户两类。

2.3 实验设计与算法评测

这一部分进行了一个简单的离线测试。

2.3.1 数据集

MovieLens数据集。这里使用的为中等大小的数据集，包括6000多用户对4000多部电影的100万条评分，评分范围为1~5。这里研究的是TopN推荐问题。

2.3.2 实验设计

M折交叉验证。

2.3.3 评测指标

使用准确率/召回率、覆盖率进行评测，公式如下：

Recall = frac{sum_u |R(u)cap T(u)|}{sum_u |T(u)|}

Precision = frac{sum_u |R(u)cap T(u)|}{sum_u |R(u)|}

Coverage=frac{|cup_{uin U} R(u)|}{|I|}

其中，R(u)为推荐列表，T(u)为用户喜欢的列表，I是全体物品的列表，U是所有推荐列表。此外还要考虑物品的新颖度，这里考虑使用平均流行度来衡量，平均流行度越小则越新颖。

Popularity=frac{sum_{uin U} Big( sum_{iin R(u)}log big(1 + Pop(i)big)Big)}{sum_{uin U}|R(u)|}

其中Pop(i)表示物品i的流行度，一般即为该物品在数据集中出现的频次。取对数是为了增加数值稳定性。

2.4 基于邻域的算法

2.4.1 基于用户的协同过滤算法

2.4.1.1 基础算法（UserCF）

主要步骤：

    找到与目标用户兴趣相似的用户集合找到这个集合中的用户喜欢的，且目标用户没有听说过的物品推荐给目标用户。

一个关键步骤是计算两个用户的兴趣相似度，采用如下公式：

w_{uv} = frac{|N(u)cap N(v)|}{|N(u)cup N(v)|}

即交并比，或者余弦相似度：

w_{uv} = frac{|N(u)cap N(v)|}{sqrt{|N(u)|cdot |N(v)|}} （我也不太明白为什么这个公式叫做余弦相似度）

按照这个公式两两计算相似度的话时间成本太大，考虑到许多情况下上式分子为0，因此可以考虑先把所有不为0的分子计算出来，然后除以分母，就可以得到相似度矩阵了。

具体做法为，先建立一个从物品到用户的倒排表，对每个物品都保存对其操作过的用户列表。可以扫描此表，假设扫描到物品i，对应的用户列表中，对于任意两个用户u和v，则相似度矩阵上二者的值W[u][v]与W[v][u]均加一。扫描完整个列表就可以得到所有用户之间不为0的W[u][v]。然后可以逐行逐列分别除以 sqrt{|N(u)|} ，就可以得到最终的相似度。

得到相似度以后，就可以向当前用户推荐与其兴趣最相似的K个用户喜欢的物品。具体做法为，选取与当前用户u兴趣最相似的K个用户，将这些用户喜欢列表中用户u没有操作过的取出，并且进行打分，打分公式为：

p(u,i)=sum_{vin S(u,K)cap N(i)} w_{uv}r_{vi}

左边为用户u对物品i的感兴趣程度，右边为加权和，即在与用户u最相似的K个用户中，找到对物品i操作过的用户，计算这些用户对物品i的兴趣（因为这里是单一行为的隐反馈数据，因此兴趣值 r_{vi} 均为1，权重则是用户u与这些用户的相似度。

实验结果略。

2.4.1.2 相似度计算的改进（User-IIF）

上面对兴趣相似度的计算基于这样一个假设，即如果两个用户购买了相同的商品，则他们的兴趣是相似的。但是这里存在一个问题，即热门物品与冷门物品在相似度计算上的贡献是相等的，然而两个购买了《新华字典》的人的相似度应当小于购买了《数据挖掘导论》的两个人，因为很多人都买过《新华字典》而《数据挖掘导论》却只有少数人买。因此，要基于物品的流行程度对相似度计算进行修正，John S. Breese在论文中提出的公式如下：

w_{uv} = frac{sum_{iin N(u) cap N(v)} frac{1}{log(1+|N(i)|)}} {sqrt{|N(u)|cdot |N(v)|}}

即在分子上，原本每一个相同物品的权重为1，现在使用一个分式代替。物品i的流行度越高，权重越小。

2.4.2 基于物品的协同过滤算法

2.4.2.1 基础算法

基于用户的协同过滤算法在用户量很大的情况下计算和存储开销很大，而且很难对推荐结果做出解释。基于物品的协同过滤算法(ItemCF)在此背景下被提出，用来向用户推荐与他们之前喜欢的物品相似的物品。

主要步骤：

    计算物品之间的相似度根据物品的相似度与用户的历史行为给用户生成推荐列表

这一算法与基于用户的算法大致步骤相同，只是相似度计算的对象变为了物品。如果购买了商品i的用户常常也购买商品j，那么我们认为商品i与商品j是相似的。基于这一假设，可以使用以下公式计算商品i对商品j的相似度（i对j与j对i是不同的）：

w_{ij}=frac{|N(i)cap N(j)|}{|N(i)|}

但是如果商品j非常热门，那么购买了商品i的用户很有可能购买了商品j，计算出来的相似度会趋近于1。这就会导致所有物品都与热门物品有很高的相似度。因此，需要对相似度计算进行修正：

w_{ij} = frac{|N(i)cap N(j)|}{sqrt{|N(i)|cdot |N(j)|}}

这样的话，这里的相似度公式与基于用户的公式大致相同了。

这里蕴含的假设是：每个用户的兴趣局限在某几个方面，因此如果某个用户购买了两件商品，这两件商品就可能属于这几个有限的领域。当很多用户都购买了这两件商品时，那么这两件商品就更可能属于同一个领域，因而具有较大的相似度。

算法与基于用户的算法类似，也是建立倒排表，不过这里的倒排表是从用户到物品。兴趣度的公式也是类似的：

p(u,j)=sum_{iin S(j,K)cap N(u)} w_{ji}r_{ui}

2.4.2.2 用户活跃度对物品相似度的影响

考虑这样一个用户，他是开书店的，购物车中包含着某网站上80%的商品。假设一共有100万本书，根据上面的公式计算，这80万本书之间就产生了相似度，因而会产生一个80万×80万的稠密矩阵。此外，这个用户虽然活跃，但是其对相似度的贡献应当小与一个只购买了少数书籍的文学青年。因此，John S. Breese提出了IUF(Inverse User Frequency)，即用户活跃度对数的倒数的参数，认为活跃用户对物品的相似度的贡献应当小于不活跃用户，修正以后的公式如下：

w_{ij} = frac{sum_{uin N(i) cap N(j)} frac{1}{log(1+|N(u)|)}} {sqrt{|N(i)|cdot |N(j)|}}

实际情况中，为了避免相似度矩阵过于稠密，往往直接忽略该用户。

2.4.2.3 物品相似度的归一化

Karypis的研究中发现，如果将ItemCF的相似度矩阵按最大值归一化，可以提高推荐的准确率。归一化公式：

w'{ij}=frac{w{ij}}{underset{j}{max} w_{ij}}

直观来看，就是将相似度矩阵中的值除以该列的最大值。那么商品i到其他所有商品的相似度的比较都在同一个水平上了。

归一化除了增加准确率以外，还可以增加推荐的覆盖率与多样性。举一个例子，假设在一个电影网站中，有两种电影——纪录片和动画片。那么，ItemCF算出来的相似度一般是纪录片和纪录片的相似度或者动画片和动画片的相似度大于纪录片和动画片的相似度。但是纪录片之间的 相似度和动画片之间的相似度却不一定相同。假设物品分为两类——A和B，A类物品之间的相似 度为0.5，B类物品之间的相似度为0.6，而A类物品和B类物品之间的相似度是0.2。在这种情况下， 如果一个用户喜欢了5个A类物品和5个B类物品，用ItemCF给他进行推荐，推荐的就都是B类物品， 因为B类物品之间的相似度大。但如果归一化之后，A类物品之间的相似度变成了1，B类物品之 间的相似度也是1，那么这种情况下，用户如果喜欢5个A类物品和5个B类物品，那么他的推荐列 表中A类物品和B类物品的数目也应该是大致相等的。从这个例子可以看出，相似度的归一化可 以提高推荐的多样性。

一般来说，热门的类其类内物品相似度一般比较大。如果不进行归一化，就会推荐 比较热门的类里面的物品，而这些物品也是比较热门的。因此，推荐的覆盖率就比较低。相反， 如果进行相似度的归一化，则可以提高推荐系统的覆盖率。

2.4.3 UserCF与ItemCF的比较

一般来说，UserCF的推荐更社会化，反映了用户所在的 小型兴趣群体中物品的热门程度，而ItemCF的推荐更加个性化，反映了用户自己的兴趣传承。

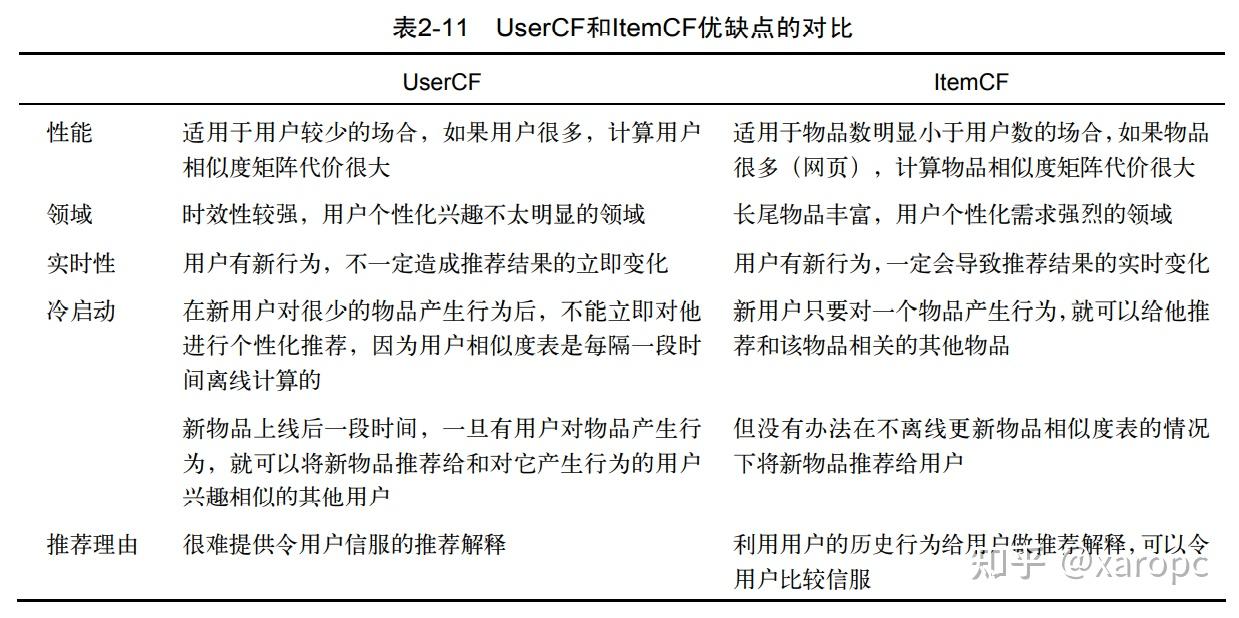
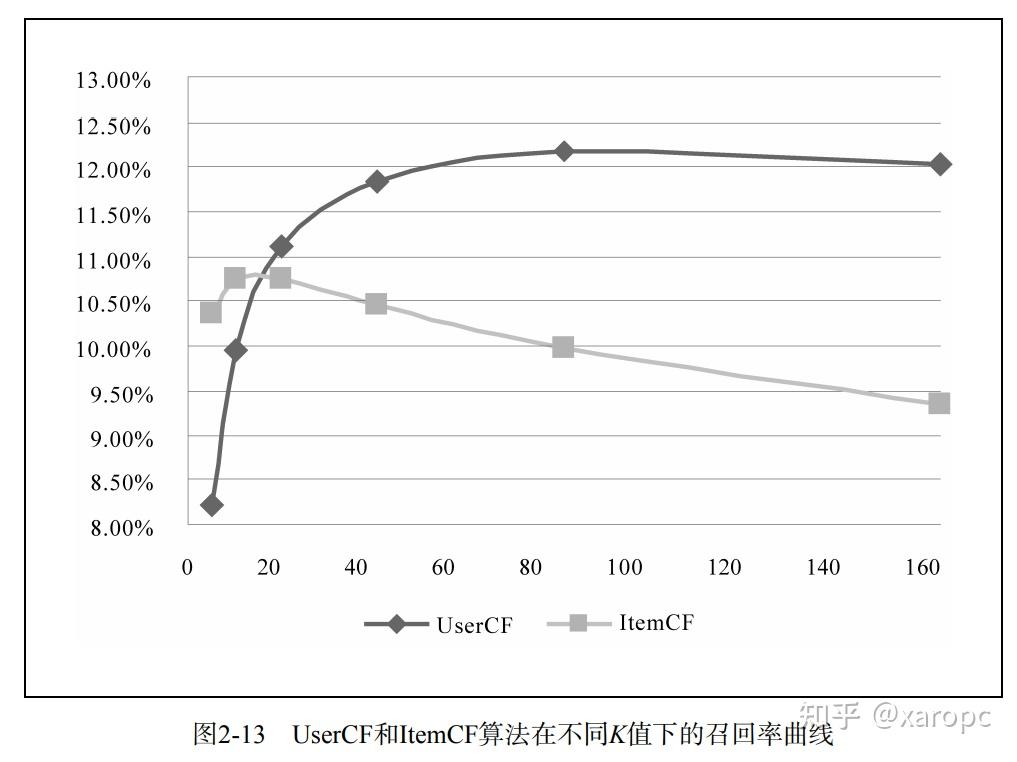
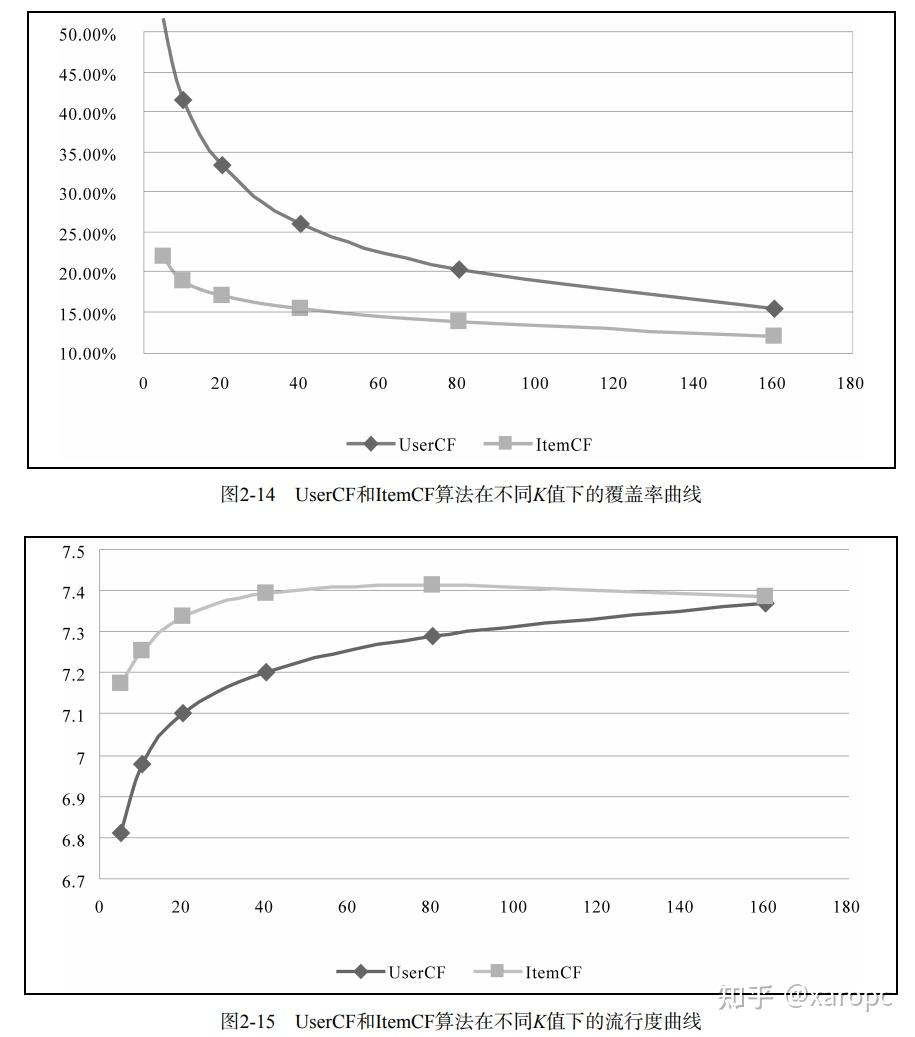
单从离线结果上看，似乎UserCF在召回率、覆盖率上有优势，但是在流行度上表现不如ItemCF。不过离线指标并不起决定作用，用户人数、商品数量、推荐解释往往更加重要。

哈利波特问题

购买任何一本书的人似乎都会购买哈利波特。因此要加大对热门物品的惩罚，对相似度公式进行修正：

w_{ij} = frac{|N(i)cap N(j)|}{|N(i)|^{1-alpha}cdot |N(j)|^{alpha}}, alphain [0.5,1]

这里假设j是是更热门的物品。一般来说，α越大，覆盖率就越高，平均热门程度会降低。

2.5 隐语义模型(LFM, Latent Factor Model)

2.5.1 基础算法

隐语义模型的核心思想是在用户与商品间建立一个中间特征。举个例子，如果我们知道用户u最喜欢的话题是武侠小说，与武侠小说关系最大的商品则是《天龙八部》，那么我们就可以向这个用户推荐《天龙八部》。当然，这里的话题或特征都是通过数据挖掘得出的，并不是人为规定好的。

LFM通过如下公式计算用户u对物品i的兴趣：

Preference(u, i) = r_{ui} = p^T_{u}q_i=sum^F_{f=1}p_{u,k}cdot q_{i,k}

上述公式涉及两个参数矩阵， Pin R ^{Ktimes U} 与Qin R ^{Ktimes I} ，其中P衡量用户与特征的关系，Q衡量商品与特征的关系。

当数据集是隐式反馈数据集时，如何构造负样本成为一个值得考虑的问题。一般来说，应当遵循以下原则：

对于每个用户，应当保证正负样本的平衡（数目相似）。对每个用户采样负样本时，要选取那些很热门但是用户却没有采取行为的物品。

这里如果(u, i)是正样本，则 r_{ui}=1 ，否则为0。接下来需要优化这一损失函数：

C=sum_{(u,i)in K}(r_{ui}-hat{r}{ui})^2 =sum{(u,i)in K}Big(r_{ui}-sum^K_{k=1}p_{u,k}cdot q_{i,k} Big)^2 + lambda||p_u||^2+lambda||q_i||^2 就是一个平方差损失函数，加上了正则化项。一般采用随机梯度下降进行优化。

2.5.2 实例

雅虎曾经以CTR为目标利用LFM预测。遇到的问题是无法实时推荐，因为LFM需要反复迭代才能有较好的性能，而且在新闻领域存在冷启动问题。他们使用这一公式进行计算：

r_{ui}=x^T_ucdot y_i + p^T_ucdot q_i

其中，x_u是用户u对各个话题的感兴趣程度，每天计算一次，y_i是基于新闻i的内容属性得到的特征向量。而p_u,y_i则是根据实时拿到的用户的最近几小时的行为训练LFM获得。因此对于新加入的新闻i，可以通过前半部分计算感兴趣程度，几个小时后就可以使用后半部分更加精确地预测。

2.5.3 LFM与基于邻域方法的比较

理论基础：LFM理论基础更好，是一种学习方法；邻域方法是一种统计方法。离线计算的空间复杂度：用户相关表需要O(M*M)的空间，物品相关表需要O(N*N)的空间。LFM如果建立了F个类，则需要O(F*(M+N))的空间。离线计算的时间复杂度：假设有M个用户，N个物品，K条用户对物品的行为记录，则UserCF计算用户相关表的时间复杂度为O(N*(K/N)^2)，ItemCF计算物品相关表的时间复杂度为O(M*(K/M)^2)。对于LFM，如果存在F个隐类，迭代S次，计算复杂度为O(K*F*S)。一般情况下，二者没有本质差别。在线实时推荐：UserCF与ItemCF都需要将相关表存在内存中，可以进行实时预测。而LFM实时预测的开销很高，如果返回权重最大的N的物品，时间复杂度为O(M*N*F)。因此LFM不太适合物品数非常庞大的系统，如果用也需要先计算一个较小的候选列表。一般来说，LFM不能在线实时推荐。推荐解释：ItemCF可以推荐解释，LFM无法解释，隐类很难用自然语言描述。

2.6 基于图的模型

2.6.1 用户行为数据的二分图表示

可以将用户对物品的行为转变为二分图表示，圆形节点表示用户，方形节点表示商品，连线代表行为。

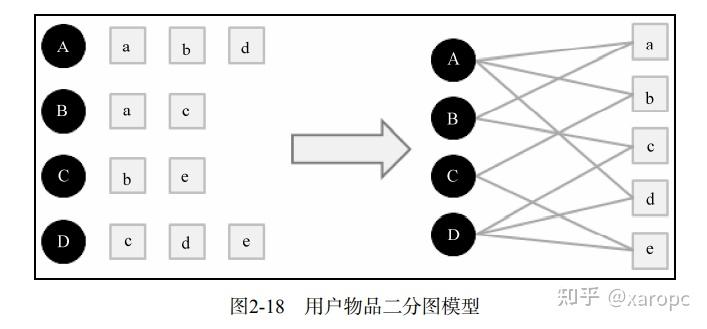
2.6.2 基于图的推荐算法

在二分图上，给用户u推荐物品的任务就变成了度量用户节点v_u与其他没有边相连的物品节点的相关性，并以相关性的高低来排列推荐表。

基于随机游走的PersonalRank算法。假设要给用户u进行个性化推荐，可以从用户u对应的节点v_u开始在用户物品二分图上进行随 机游走。游走到任何一个节点时，首先按照概率α决定是继续游走，还是停止这次游走并从 v_u节点开始重新游走。如果决定继续游走，那么就从当前节点指向的节点中按照均匀分布随机选择一 个节点作为游走下次经过的节点。这样，经过很多次随机游走后，每个物品节点被访问到的概率会收敛到一个数。最终的推荐列表中物品的权重就是物品节点的访问概率。

迭代计算访问概率的公式如下：

PR(v)=(1-alpha)t+alphasum_{v'in in(v)}frac{PR(v')}{|out(v')|}, t = I(v=v_u)

其中，α表示继续游走的概率，in(v)表示所有指向v的节点集合，out(v)表示v指向的所有节点的集合。公式的解读可以参照这篇博客推荐系统4——图模型（PersonalRank），大意是前面的(1-α)t表示不进行游走的概率，这里把这一部分概率都放在了初始节点上。因为在计算时，其他所有节点的概率都是从初始节点中分出的，而当我们返回利用公式计算初始节点的概率时，剩下的没有分出去的概率之和就为1-α，需要加上。

这一算法虽然理论解释性好，但是计算时间复杂度高，不仅无法在线实时推荐，而且离线计算也很耗时。解决方法是将PersonalRank的迭代转化为矩阵形式，假设M是二分图的转移概率矩阵，即

M(v,v')=frac{1}{|out(v)|}

也就是认为从当前节点转向其指向的节点是等可能的，那么迭代公式可以变为：

begin{aligned} r &= (1-alpha)r_0+alpha M^T r iff r &= (1-alpha)(I-alpha M^T)^{-1}r_0 end{aligned}

这里的r与r_0均为向量，分别表示当前的节点访问概率分布与初始节点访问概率分布。方程描绘了访问概率收敛的条件，因此只需要计算一次并求逆即可。

文章标题: 《推荐系统实践》笔记 第二章 利用用户行为数据
文章地址: http://www.xdqxjxc.cn/duhougan/126229.html
文章标签：推荐系统实践（书籍）  推荐系统  读书笔记
Top