欢迎访问喜蛋文章网
你的位置：首页 > 读后感 > 文章正文

《统计学的世界》[第8版] Chapter3:样本可以告诉我们什么？——读书笔记

时间: 2021-06-11 09:26:25 | 作者：Yeun | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 100次

《统计学的世界》[第8版] Chapter3:样本可以告诉我们什么？——读书笔记

01 从样本到总体

参数(Parameter)：是描述总体的数字。参数是一个固定数值，但我们无法知道参数的实际值。一般我们用 p 表示。

统计量(statistics)：是描述样本的数字。一旦有了样本，统计量的值即可得知，如果换一个样本，统计量的值就可能有所改变。我们常用统计量来估计未知的参数。一般我们用 P ̂ 表示。

那么，参数和统计量的具体区别到底在哪？我们试着引入如下例子来说明。

Example1：同性恋是否应得到法律认可的民意调查

同性婚姻一直富有争议性，许多人基于宗教信仰表示反对。反对者认为同性婚姻破坏了传统的家庭和婚姻制度，支持者认为这涉及权利平等问题。2004年2月，这个话题在美国成为重大新闻，受到全国人民的关注。在一些城市——其中最知名的是旧金山市——出现了同性婚礼，尽管这违反了该州的法律。小布什总统对此发表讲话说：“今天，我建议国会尽快通过并送交各州推行一项宪法修正案，该修正案承认和保护婚姻是男女双方以夫妻名义形成的联合体。”关于这项修正案，有多少人支持呢？一项从2003年7月到2004年2月进行的盖洛普民意调查提出问题：“你支持还是反对宪法修正案规定只有男女才能结婚，而不允许男同性恋者和女同性恋者建立婚姻关系？”该项调查发现，“支持该宪法修正案的人为51%，略高于45%的反对者比例”。这是在随机访谈了2527名美国成年人后得出的结论。盖洛普公司采用了随机抽样的方式，与只访谈那些参加旧金山市同性婚礼的人相比，调查结果的偏差会更小。

这个例子中，2527位成年人的样本是随机抽取的，样本代表的总体是2.2亿的全美成年人。我们有理由相信，这个样本可以比较好地代表总体，并且估算出“所有成年人”中约有51%的人支持该修正案。

这代表了统计领域的一种基本做法：用抽样调查的结论，当作对总体真实信息的估计。

另外，解答上面提出的两个概念。统计量就是在样本量为2527位美国成年人下，支持宪法修正案的比例为51%，“51%”即样本的统计量。

参数之于总体，参数的实际值我们并不清楚。那么，我们会用样本的统计量当作参数的估计值，也是“51%”。

我们继续看进一步的解释：

所有支持该宪法修正案的调查对象的比例，就是描述约2.2亿美国成年人这一总体的参数。我们将其记作 p ，意为“比例”(Proportion)。但是，我们无法知道它的确切数值。为了估算出p 的值，盖洛普公司抽取了一个包含2527位成年人的样本。该样本中支持者的比例就是 p 的估计值，记作 P ̂ ，读作“戴帽子的p”。因为在2527人中有1289人支持修正案，所以对于这个样本，有如下样本量统计值：

样本量统计值为51%

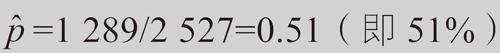
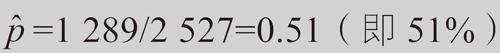
由于所有成年人都有同样概率被选入2527的样本，因此，我们可以用统计量P ̂=0.51作为未知参数 p 的估计值。

02 样本统计量的变异性

偏差：当我们取多个样本时，它们的统计量朝同一个方向偏离总体的参数值。

变异性：当我们取多个样本时，统计量的值的离散程度。变异性大，意味着不同样本的统计量可能差别也较大。一个好的抽样方法，其偏差与变异性都较小。

接着上述的例子，如果盖洛普公司重新抽取一个2527人的随机样本，那么这个样本会包含于前一个样本不一样的人。几乎可以肯定的是，不会有1289人给出支持的答复。也就是说，统计量P ̂的值，会随着样本的改变而改变。一个随机样本说有51%的美国成年人支持宪法修正案，而另一个随机样本说只有37%的人支持修正案。

第2章已经说明，随机样本可以有效地消除偏差，但是由于随机选取的样本有变异性，所以调查结果可能还是不准确。

那么，如何解决变异性的问题？

答案：扩大样本量。

统计学另外一个很重要的概念是：要知道一个样本有多可靠，就得问问如果我们从同一总体中抽取多个样本，会出现什么情况。

还是接着盖洛普民意调查的例子，我们假设正好有50%的美国成年人支持这项宪法修正案（盖洛普不知道）。也就是说，总体的参数p = 0.5。

如果盖洛普公司用大小为100的简单随机样本得出的P ̂来估算总体的p，会怎么样？

我们来看下面的解释过程：

假设我们每次抽取的样本量为100，反复抽取1000次，得出不同的P ̂值。如下图所示，第一个样本中，100人有56人支持修正案，因此P ̂=56/100=0.56。在下一个样本中，只有36人支持修正案，因此该样本的P ̂=36/100=0.36。

选出1000个样本，将其计算出的P ̂绘制成柱状图。横轴代表不同的P ̂值区间，柱形高度代表1000个样本中，有多少个落在相应的横轴区间。

例如，在图上，P ̂值为0.40~0.42的柱形高度略微超过50，这意味着1000个样本中有50个以上的样本的P ̂值为0.40~0.42。

图3-1，可以看到P ̂值会落在以p=0.5为中心的范围内

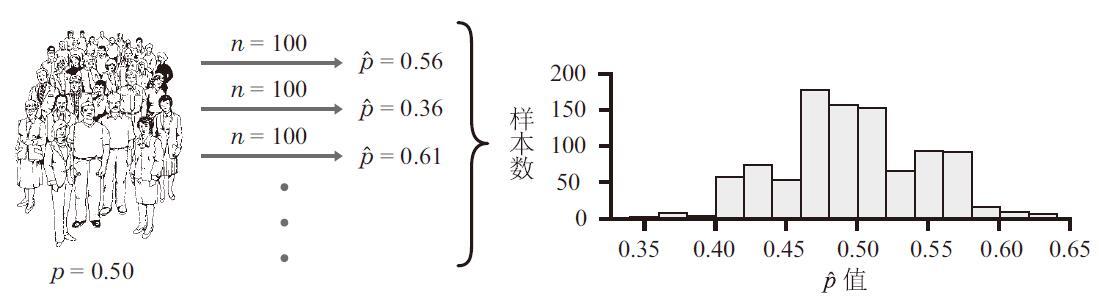
现在，我们试着将单次样本量扩大为2527个，反复1000次，得到如下的柱形图：

图3-2

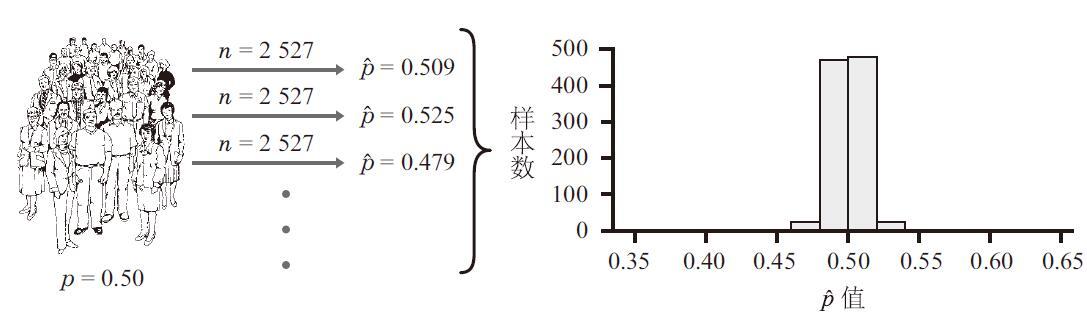
对比这两幅柱状图，单次样本量更大所得到的1000个P ̂值，和图3-1相比，P ̂的分布范围要窄得多。

由此我们有如下结论：

    对于上面这两种情况，样本的P ̂值会随着不同的样本而变化，但都以0.5为中心，0.5是总体的p值。有些样本的P ̂值比0.5小，有些比0.5大，但并不会都比0.5大，或都比0.5小。大小为100的多个样本的P ̂值的分布情况，会比大小为2527的多个样本的P ̂值要分散得多。事实上，在大小为2527的1000个样本当中，有95%的P ̂值分布在0.4805~0.5195的区间内。也就是说，与0.5的差距在±0.0195的范围内。而在大小为100的1000个样本中，有95%的P ̂值分散在0.40~0.60的范围内，与0.5有±0.1的差距，约为大样本的5倍。所以，大样本统计量的变异性要比小样本小。我们可以信任一个大小为2527的样本，其统计量的值几乎总会很靠近总体的p值。而大小为100的样本，在p值是50%的时候，有可能得出为40%或60%的估计值。

那么，我们如何处理偏差与变异性呢？

减少偏差的方法：使用随机抽样方法。（第2章已经详细说明）

减少变异性的方法：扩大样本量。

03 误差范围

误差范围(margin of error)为±2%的具体意思是：

如果我们用抽取这个样本所用的方法，去抽取多个样本，那么这些样本的统计量中有95%会在总体参数真实值的正负两个百分点的范围之内。

误差范围用于描述样本的统计量P ̂的变异性，是关于调查结果的可信度叙述。

Example2：电视新闻

电视新闻播音员说：“最近发布的一项盖洛普民意调查发现，约有51%的美国成年人支持小布什总统关于婚姻的宪法修正案，反对同性婚姻。此次调查的误差范围是±2%。”51%加减两个百分点，分别是53%和49%，总体对该修正案的真正态度落在这个区间之内。而盖洛普公司实际上说的是：“对于该抽样调查的结果，我们有95%的信心认为，由抽样或其他随机因素造成的误差，应该在正负两个百分点之间。”也就是说，该误差范围只适用于95%的样本统计量，“95%的置信度”就是这种意思的简单表达，而新闻报道中把“95%的置信度”漏掉了。

回到盖洛普民意调查的例子，盖洛普的民意调查访谈了2527人，对应95%的置信度。根据误差速算法公式，如果置信度为95%，那么误差大致在

1/√n

由此公式，得：

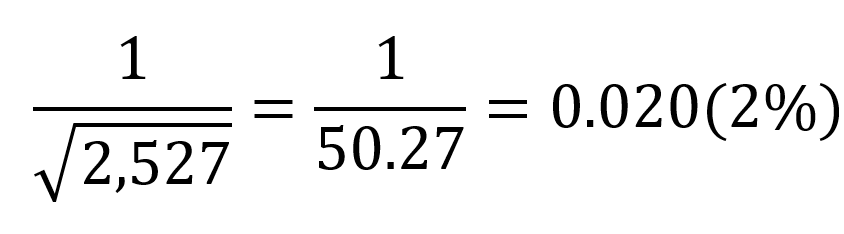
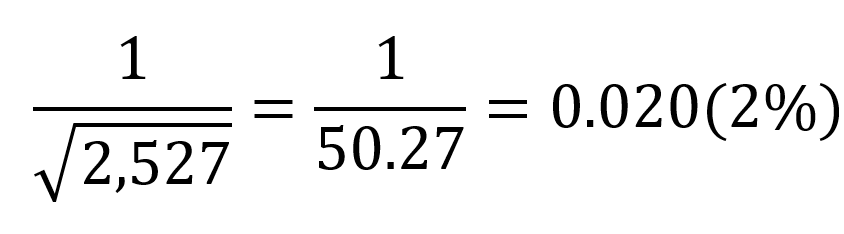
这与Example2所述的误差范围吻合。

另外，我们仔细地查看这个公式，可以得知：

    当n值越大，得出的误差范围就越小。因为公式用的是样本大小的平方根，若误差范围减半，n值应该扩大4倍。即用4倍原来大小的样本量。

再看当单次样本量为100时，误差范围是：

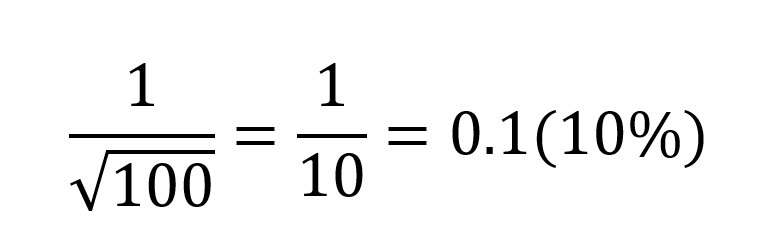
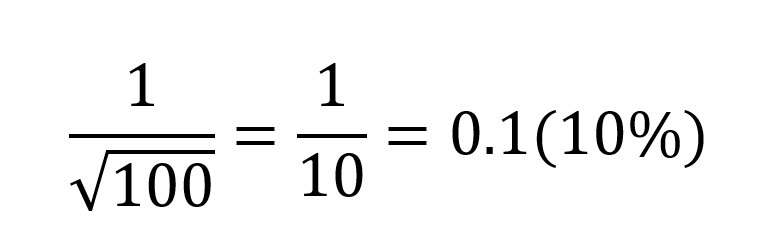
因为2527大约是100的25倍，25的平方根是5，因此，100人样本的误差范围约为2527人的5倍。

04 关于置信度

置信度说明：

包含两个部分：误差范围与置信度（level of confidence）。误差范围告诉我们，样本统计量距离总体参数真实值有多远。置信度告诉我们，所有样本统计量中，满足该误差范围的样本统计量的百分比。

关于Example2的置信度说明，我们可以简化说法为：“我们有95%的把握认为，在所有成年人当中，有49%~53%的人支持该修正案。”，这就是置信度说明。

注意：

    置信度说明的是总体而不是样本。我们对总体所做的结论不可能完全正确。盖洛普公司调查所用的样本有可能使误差超过两个百分点的5%样本之一。抽样调查也可以选择95%之外的置信度。例如我们可以选99%的置信度，但代价是，误差范围会扩大。

05 总体的大小

一个随机样本统计量的变异性，不受总体大小的影响，只需确保总体至少比样本大100倍即可。

假设我们从已收获的玉米种抽样，把勺子插进玉米粒当中。勺子并不知道它是在一袋玉米当中，还是在一卡车的玉米当中。如果玉米混合得很均匀（如此一来，勺子舀出来的玉米就是随机样本），样本统计量的变异性就只与勺子的大小有关。

如果我们要估计俄亥俄大学中在政治方面属于保守派的学生比例，还是要估计美国所有成年人中的保守派人士的比例，只要两者要求同样的误差范围，就得抽取一样大的简单随机样本。（因为样本量的变异性首样本量大小影响）要知道，俄亥俄大学只有4.9万名学生，而2009年美国成年人口超过2.32亿。这说明，在俄亥俄大学中抽取的样本占总体的比例要高得多。

文章标题: 《统计学的世界》[第8版] Chapter3:样本可以告诉我们什么？——读书笔记
文章地址: http://www.xdqxjxc.cn/duhougan/109074.html
文章标签：统计学  应用统计学  读书笔记
Top