欢迎访问喜蛋文章网
你的位置：首页 > 经典文章 > 文章正文

【硬核科普】最小作用量原理：宇宙的设计图

时间: 2021-08-03 16:27:05 | 作者：RHY | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 122次

【硬核科普】最小作用量原理：宇宙的设计图

不同领域的物理学规律之间很难直接找到联系之处，但最小作用量原理却可以将大多数物理定律纳入一个很高的思想体系之中。如果说最小作用量原理是宇宙的设计图，那么对称性就是这张设计图的规范标准，作用量总是需要满足某些对称性要求。尽管最小作用量原理还无法推导出诸如热学在内的一些物理规律，它仍然是最有希望用来描述整个宇宙的最高原理。

人类目前所建立的物理学定律大多数都是由常微分方程或是偏微分方程进行描述的，例如我们在小学二年级已熟知的牛顿第二定律：

F=mfrac{d^2r}{dt^2}

它可以用来描述低速宏观物体的机械运动。再如麦克斯韦的电磁场理论：

实在是懒得打字…

它揭示了宏观电、磁、光的统一性。还有薛定谔方程：

它告诉我们描述微观粒子的概率波是什么样子的。

这些方程在各自的领域内无疑是强有力的，它们对自然界的概括和对其本质的揭示远胜于一条条唯象物理定律的堆砌。然而这些定律都有其适用范围，并且不同领域的物理定律之间几乎毫无关联——上述三条式子，没有哪一条是可以由另外两条定律推导出来的。

这种物理定律之间的隔离性并不是我们想看到的，我们总是希望找到能够在大多数甚至是全部的物理过程中普遍成立的原理。爱因斯坦就曾经说过：“我想知道上帝是如何设计这个世界的，对这个或那个现象、这个或那个元素的谱我不感兴趣。我想知道的是他的思想，其他的都只是细节问题。”

在经过大量的实验总结和检验以后，我们有理由认为，最小作用量原理就是这么一个能够较为普遍成立的原理，是物理定律的定律，是宇宙的设计图纸。

一、自然界中的极值

最小作用量原理具有极为深刻的科学与哲学内涵，其思想源于自然界中各种极值现象。例如：水珠在失重的环境下会呈现出球形，以使得表面张力能最小；热力学系统总是朝着熵增的方向演化，直到到达某个极大值；光在行进的过程中总是使得光程取极大或极小值；将一个歪七扭八的金属导体放入一个奇形怪状的静电场中去看它的面电荷分布，尽管算力最强的计算机也要花上一段时间来模拟出近似的结果，自然界却几乎能够无延迟得给出电荷排布，以使得总体能量最小。

正如最小作用量原理最开始是朦胧、模糊的观念一样，以上种种也仅仅只是对各类现象的定性总结，远远谈不上定量化的具有完美数学表达式的物理学基本原理。然而从上述现象中我们仍然可以发现，宇宙似乎是个精明的商人，它总是尽心设计物理定律，使得“成本”最小——尽管这样说似乎有一种神学的味道。

二、哈密顿原理

17世纪至18世纪，最小作用量的思想在历经费马、欧拉、拉格朗日、莫培督等人的洗礼后，被哈密顿发展到了一个顶峰。我们得到了一种以统一的形式和精确的数学去描述这些极值问题的原理——哈密顿原理（Hamilton's principle），它是最小作用量原理（The principle of least action）的一种表述。

在力学中，可以导出全部力学定律的原理称为力学第一性原理。牛顿运动定律就是这样的一种力学原理，但它并不是唯一的。哈密顿原理在物理学中是作为公理而存在的，依据它我们也可以建构起整个经典力学的理论体系，甚至于推广到量子力学或是相对论中，从而建立起描述几乎整个世界的理论体系。

假如我们定义作用量为拉格朗日量对时间的定积分：

S(C)=int_{t_1}^{t_2}L(mathbf q(t),dot{mathbf q}(t),t)dt

则哈密顿原理可以表述为：在 和 时间内，取等时变分 的情况下，真实运动轨迹是泛函 取极值的路径，即：

delta S(C_{12})=0

从这条极其简洁的式子出发，我们可以得到拉格朗日方程，进而构建起整个理论力学，乃至推广到非力学体系。之后的工作只是去写出不同系统的拉格朗日量或者说作用量而已。例如波动方程：

rho u_{tt}-Eu_{xx}=0

它本质上就是连续体系的拉格朗日方程。如果我们取拉格朗日密度：

l=frac{1}{2}[rho u_t^2-Eu_x^2]

则由哈密顿原理可知，该力学体系需满足：

delta S=deltaint ldxdt=0

这条式子是波动方程的等价表述。

再如选取电磁场中的带电粒子的拉格朗日量为：

突然又懒得打字

则由delta S=0可以导出带电粒子的运动方程，即：

当然，这里只考虑了场对粒子的影响，而没有考虑粒子对场的影响。实际上，完整的拉氏量应为：

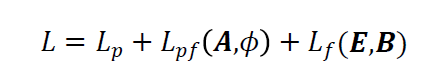
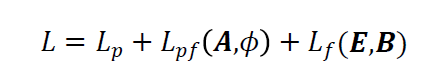
分别代表粒子、粒子和场相互作用、自由场的拉氏量,其中：

另外，值得一提的是，我们定义的作用量即使加上任意一个常数也是不改变任何物理规律的。这与最小作用量的思想也是相协调的——整体增加一个常数并不会改变极值所对应的路径。这意味着，如果我们取

不是吧，这都懒得打！

为新的拉格朗日量，对原有的物理规律并不会产生任何影响，这被称为规范不变性。如果我们对上述电磁场的拉格朗日量取下述规范变换：

实乃图文并茂

则依据最小作用量原理，

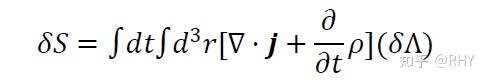
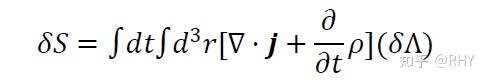
应为0.（上式省略了一些推导过程，反正写出来也没人看）

从而由于delta Lambda是任意的，我们可以得到电荷守恒方程：

nablacdotmathbf j+frac{partial }{partial t}rho=0

而这本来是由Maxwell方程组得到的。以上只是单举一例，事实上，19世纪末, 拉莫从最小作用量原理导出了麦克斯韦方程组, 从而也就导出全部电磁学的基本规律。

更一般的，选取不同的规范变换，我们可以得到诸如输运方程、热传导方程、连续性方程等等与守恒量紧密相连的PDE，这无疑是对这些方程的更为统一、更为一般、更为本质的描述。

三、量子力学路径积分

最小作用量原理也适用于狭义相对论，我们只需要找到它所对应的拉格朗日量或者哈密顿量即可：

最小作用量原理甚至可以被用来导出广义相对论。希尔伯特在1916年3月31日发表的论文就以最小作用量原理为基本出发点得到了广义相对论的引力场方程。从现代物理学的观点来看，希尔伯特的做法极具前瞻性，因为现代物理学上几乎所有基础理论的研究都是从最小作用量原理出发的。

接下来着重介绍作用量与量子力学的路径积分法的联系。量子力学中的路径积分法是由狄拉克于1933年在一篇名为《量子力学的拉格朗日函数》的文章中提出，之后由美国科学家理查德·费曼进一步发展而来。

如果我们采用牛顿力学的观点看待一个粒子，它的运动是好理解的，粒子由于受到力的作用，速度发生了变化，从而形成了不同的运动轨迹。但是，当我们用最小作用量原理重新审视这个问题的时候，情况就发生了变化：粒子怎么知道哪条路径的作用量最小呢？路径积分法便可以很好的回答这个问题。

在路径积分法诞生以前，量子力学已经有了比较成熟的两种等价表述，一是薛定谔的波动力学，二是海森堡的矩阵力学，两者都否定了粒子的轨道运动。而路径积分法的出发点则是粒子会走所有可能的路径，不同的路径会对应着不同的作用量（为简单起见，取一维情况）：

积分上限是t_b

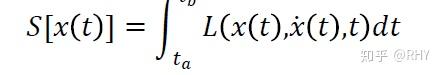
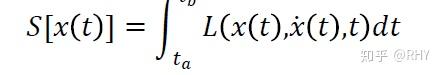
如果我们已经知道t_a时刻描述粒子的波函数Psi(x_a,t_a)，希望计算波函数演化至t_b时刻的Psi(x_b,t_b)，则应当考虑从x_a到x_b的每一条可能路径对 Psi(x_b,t_b) 的贡献，即：

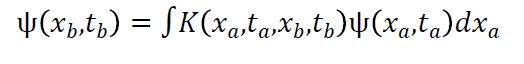
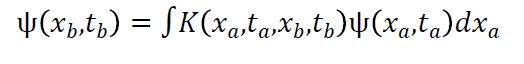
其中

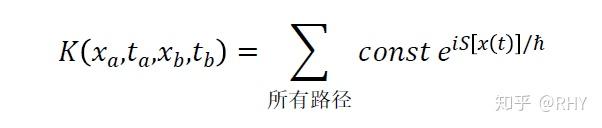
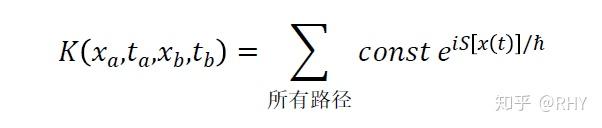
也就是说，粒子从a点到b点时（这样的说法可能不是那么严谨，但是比较方便，事实上粒子的位置是不确定的，它在不同点有着不同的出现的概率，这也是为什么我们需要对 积分），由于不确定性关系的影响，将不再只有一条和作用量有关的路径，而是具有无穷多可能的路径，并且依照实验所显示的相干效应，彼此线性叠加起来。换言之，在量子的世界中，粒子会“嗅探”所有可能的路径。

那么路径积分法如何解答我们之前的问题呢？对于宏观的物理过程来说, 近似为0，指数因子剧烈振荡，对于一般的路径而言，它们所贡献的几率幅都会和与它们临近的路径所做的贡献相互抵消，从而不会引起可观测效应。然而当

delta S[x(t)]=0

也就是作用量取极值的时候，这条路径与其临近的路径近似给出同一个作用量，从而也就给出相同的相位因子，这些路径也就不会彼此抵消了。而这样的路径，正是哈密顿原理告诉我们的，宏观粒子会选择的路径。

也就是说，在宏观世界里，粒子并不是没有“嗅探”所有路径，只是由于 ，其他路径被叠加抵消了，只有S取极值的那一条，没有被抵消而已。

四、诺瑟定理：对称性与守恒律

前文对最小作用量原理的提出及运用做了一个简要的说明，我们已经感受到了它的威力，只要选取合适的拉格朗日函数，我们可以得到近乎所有的物理学规律。然而我们马上会面临这样一个问题：如何构造出合适的拉格朗日函数？

在诺瑟定理提出以前，物理学家需要经过多次尝试才能找到所需要的拉格朗日函数的具体形式。如果这样，最小作用量原理就不能称之为一种很好的物理学研究思想，而只是一种比较有趣的一般性规律。

幸运的是，物理定律的对称性和守恒律之间有着极为深刻的联系，而物理定律的对称性会对拉格朗日函数提出限制，要求它也具有同样的对称性。依据这种联系，我们可以更加容易地写出拉格朗日函数的具体形式，也能找到所研究的物理过程中到底有哪些守恒量。

为了深刻的理解这一点，我们首先得对物理中的对称性有一个正确的认识。不同于几何中的对称性，物理学中所理解的对称性是指系统在某种变换下物理学规律不发生变化。例如时间平移对称，指的是选取的时间零点发生任意的改变也不会影响我们对系统的研究；再如空间平移对称，相当于是在说物理规律不会因为我选取的位置的变化而发生变化。

而诺瑟定理则是在说对应于这样的对称性，总是有一个守恒量与之对应。在前面所举的两个例子中，它们所对应的守恒量分别是能量和动量。这个定理也可以很容易地推广到量子力学当中。如果你可以找到一个厄米算符，它与哈密顿量对易，这必然意味着系统具有某种对称性。例如如果你发现角动量是守恒的，那系统必然是空间转动不变的——意即坐标轴的取向可以是任意的。然而如果你发现只有角动量的某个分量是守恒的，那么你很容易知道，系统至少具有一个平面旋转的不变性，但不具有空间旋转的不变性。

对于一个物理系统而言，有些对称性是很直观可以看出来的，但更多的是无法一眼就能看出来的。这个时候，我们需要思考一个问题：如何确定系统具有怎样的对称性？

同我之前所说，对称性的本质是系统在某个变换下保持相同的物理规律，而物理规律往往就是由系统的哈密顿量决定的，所以如果我们能够找到这样一种变换，它使得哈密顿量在变换前后保持不变，我们就找到了一种对称性。

提到这，我们需要引入群论的观点了。事实上，如果要深刻理解对称性与守恒量之间的关系，群论是非常有用的一个工具。群的本质是一个集合，它可以是任何事物的集合，变换也不例外——只要满足群的定义。如果我们将找到的这些能够使得哈密顿量保持不变的变换表示成群的形式，我们就能找到它的生成元，而这些生成元正是这些变换所对应的守恒量。

这样，守恒量、对称性、诺瑟定理、变换、生成元、群论便能很好的联系在一起，我们研究问题时，可以先去研究系统的对称性，依据这个对称性写出守恒量，进而简化问题的求解——这是一个至今仍在使用的研究范式。

世界的运行满足最小作用量原理，而作用量的形式又受到对称性的约束，对称性又与某个守恒定律等价。如果说最小作用量原理是宇宙的设计图，那么对称性就是在设计宇宙时所需满足的标准。

五、结语

尽管最小作用量原理令人着迷，但目前仍未从最小作用量原理满意地推导出热力学定律。这或许是因为热力学过程是不可逆过程，时间具有不对称性。实际上，可能不止热力学过程是不可逆的。量子力学中有一个玄妙的定理，认为CPT（charge conjugate, parity transformation, time reversal）是联合对称的，然而在1946年，人们观测到了CP联合对称被打破，这意味着T(时间反演)也是不对称的。关于这些物理现象，可能就难以以最小作用量原理来描述了。

另外，自19世纪60年代以来，非线性科学如混沌学成为研究热点，而依赖于波函数线性叠加的最小作用量原理可能会在这方面受到限制。但不管怎么说，最小作用量原理不仅把已知的几乎所有物理学规律，甚至把未知的物理学规律都纳入到一个思想体系中，而且还体现出自然界的简洁、对称与优美，其高度的统一性与和谐性无疑使其成为物理学的最高理论。

参考文献

[1]王晓光.理论力学及其专题分析（2021版）.浙江大学物理学系本科课程讲义

[2]王凯.氢原子物理.浙江大学物理学系本科课程讲义

文章标题: 【硬核科普】最小作用量原理：宇宙的设计图
文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/118103.html
文章标签：物理学  物理科普  理论物理
Top