【知识仓库】势能与势

时间: 2021-06-08 10:27:50 | 作者：爱XR的麦子 | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 111次

【知识仓库】势能与势

势能（续）

机械能可分为动能和势能。在能量一文中提到过势能的概念来源于保守力，

爱XR的麦子：【知识仓库】能量与功zhuanlan.zhihu.com

而当我们能得到一个势能，也能从中得到它对应的力。

vec F = -vec nabla U

对于3D而言， $vec nabla = begin{pmatrix} frac{partial}{partial x} frac{partial}{partial y} frac{partial}{partial z} end{pmatrix}$ ，代表一个标量函数的梯度（Gradient）

而上文中也提到了一个约定俗成的概念

你必须做正功将一个物体移动到高势能的位置；而如果是场做功则会将物体移动到低势能的位置

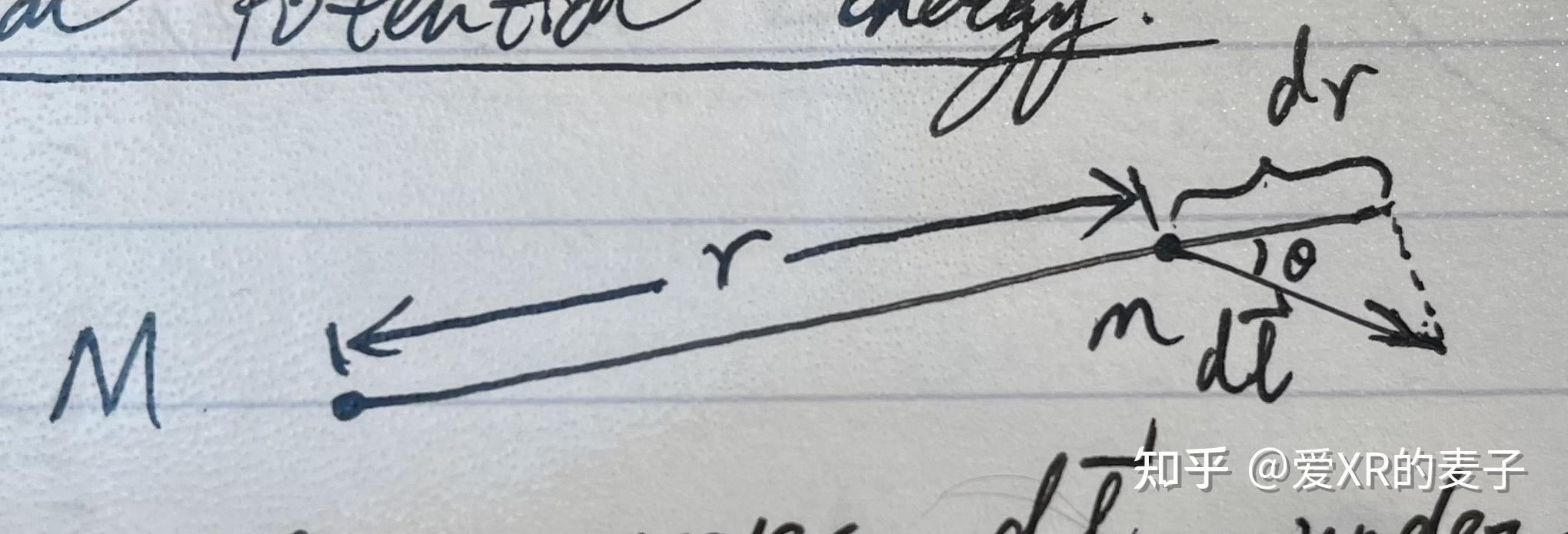
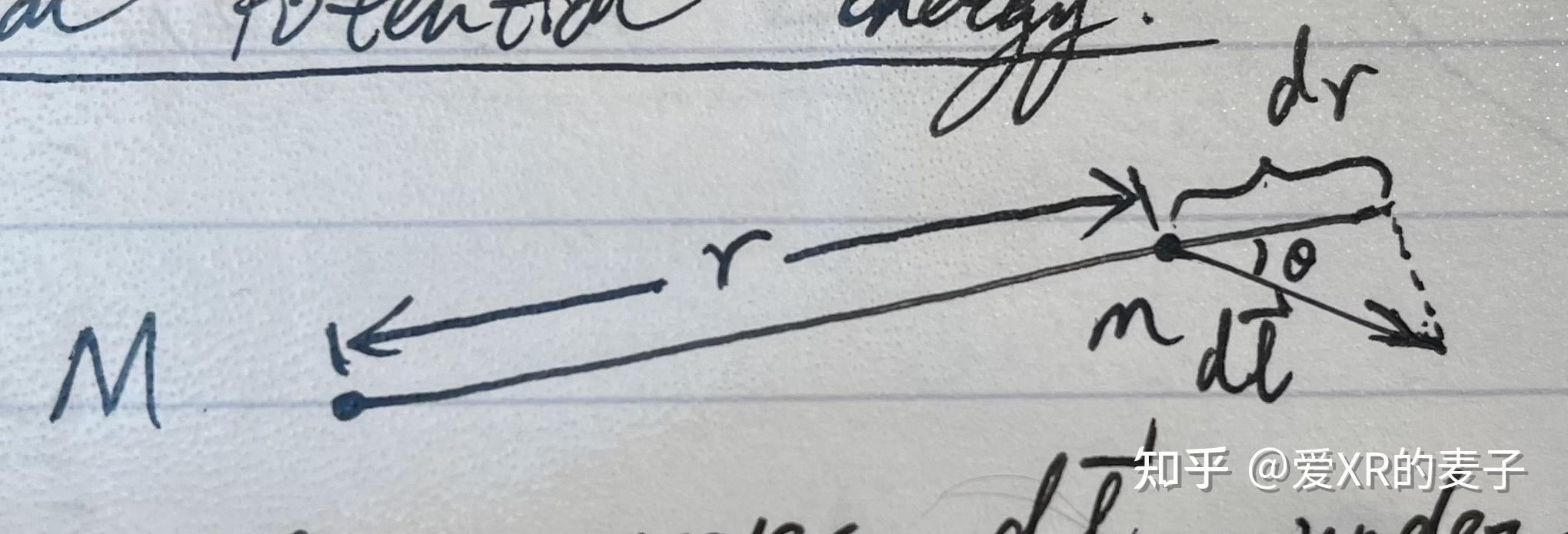
若有一个小质量在大质量的重力场下移动了 dvec l ，那么做功为

$dW = vec F cdot d vec l = -frac{GMm}{r^2} hat{r} cdot d vec l$

其中 dvec l 只有与重力场方向 hat {r} 一致的部分做功，因此

$dW = -frac{GMm}{r^2} dr$ ，

hat{r} cdot dvec l = left| hat{r} right| left| dvec l right| {cos(theta)} = dr

对于移动了一段距离而言，总的做功为

$W =-GMm int_{r(A)}^{r(B)} frac{1}{r^2} dr = GMm (frac{1}{r(B)} - frac{1}{r(A)})$

此时做功是一个只跟也就是位置有关的函数，因此重力是一个保守力，它的势能是

$U(r) = -frac{GMm}{r} + {const.}$

而这里的常数并不是一个特定值，是可以随意定义的（对于能量而言，差值比绝对值要重要）。当然，习惯性的会做这样的设定 U(r rightarrow infty) = 0 ，因此

$U(r) = -frac{GMm}{r}$

重力势一般指

某个位置上，单位质量的重力势能

$phi(r) = frac{U(r)}{m} = -frac{GM}{r}$

文章标题: 【知识仓库】势能与势

文章地址: http://www.xdqxjxc.cn/jingdianwenzhang/108625.html

文章标签：物理科普重力笔记

最新经典文章

热门经典文章

Top

全站搜索