Intro to RL Chapter 13: Policy Gradient Methods

之前的方法都是action-value methods：基于action values 来选择policy，没有value就没有policy。本章考虑直接学习parameterized policy，不需要value。可以学value function来辅助policy learning，但不需要action value 来选择action。用 来表示policy parameter vector， ， 表示value function weights。优化performance measure 来更新policy parameter： ，称为policy gradient methods。policy和value都用的叫actor-critic methods。本章先从episodic开始，performance就是value of start state，再考虑continuing case，用average reward rate作为performance measure，最后把它们联系起来。

13.1 Policy Approximation and its Advantages

policy parameter只要是differentiable，只要 存在，且对所有state，action是finite即可。实际操作中，为了保证exploration，一般要求policy不能变成deterministic。本section考虑discrete action spaces，说明policy gradient的advantages。policy-based methods 也有一些处理continuous action spaces的方法，见Section 13.7。action space是discrete且不太多时，一个常用的parameter是给每个state-action pair输出preferences ，再用softmax处理，选择preference最高的action。具体怎么得到preference就随便，可以是neural network，可以是linear function。parameterized policy + softmax一个优势是可以逼近deterministic policy，而epsilon greedy至少有有epsilon。可以用action value + softmax，但这也不能逼近deterministic，action value和直接但prob 0 / 1还是不一样但。如果softmax用temperature，应该逐渐减小来逼近deterministic。但实际操作中很难设定合适但减小速度，连temperature初始值都很难找。action preferences和action value很不同，它们不是逼近特定的值，只要是optimal action，就增大preference就好，知道infinite（如果允许的话）。parameterized policy + softmax 第二个优势是可以根据任何prob选择action。有时optimal policy可能是stochastic，比如card game，不知道全部信息，最好但policy是按一定prob选择多个action。如example 13.1，四个states，左边三个nonterminal，只有左右两个actions，第一个和第三个都正常，第二个state，选择左会走向右，选择右会走向左。state-action feature对三个states都一样。value-based methods会强制都往左或往右，而policy-based会选择合适的prob。第三个优势是有时候policy function更容易得到。有的task state少action少但policy复杂，那就用action-value methods，有的policy简单，env复杂，那就policy methods。最后，用policy function可以很方便地使用prior knowledge，这经常是使用policy-based learning但主要原因。

13.2 The Policy Gradient Theorem

除了上面的advantage，还有一些理论上的advantage。policy parameterization在action之间prob是平滑的，不像action-value based methods，action轻轻一变value就可能变化巨大。这也让policy parameter更容易converge。episodic 和 continuing case有不一样但performance measure ，虽然但是，本书尽量合起来，保证主要理论结果能用一套公式表示。本section考虑episodic case，performance measure即value of start state。假设start state一样，episodic performance： 如何优化policy parameter呢？performance不仅仅受policy影响，也有env的作用，而env的model一般不知道。幸好有 policy gradient theorem 解决，得到对于performance，policy parameter的gradient，而和env无关。policy gradient theorem for episodic case:

constant proportionality 是 average length of an episode，对于continuing case 为 1。 值on-policy distribution (see P199)。

Proof of policy gradient from Levine's course. let be a trajectory, , probability of is the probability of the whole trajectory .

13.3 REINFORCE: Monte Carlo Policy Gradient

all-actions methods, 直接从 (13.5) 得到， 用 得到的sample即follow ，对于一个step，直接更新所有的actions： REINFORCE 只update使用的action ，用sample代替 (13.6) 的expectation：

得到policy parameter update:

REINFORCE完成episode后才更新，看起来像是个Monte Carlo (gradient 改成用sum of ln，加上discounting):下图为REINFORCE 在 example 13.1 的结果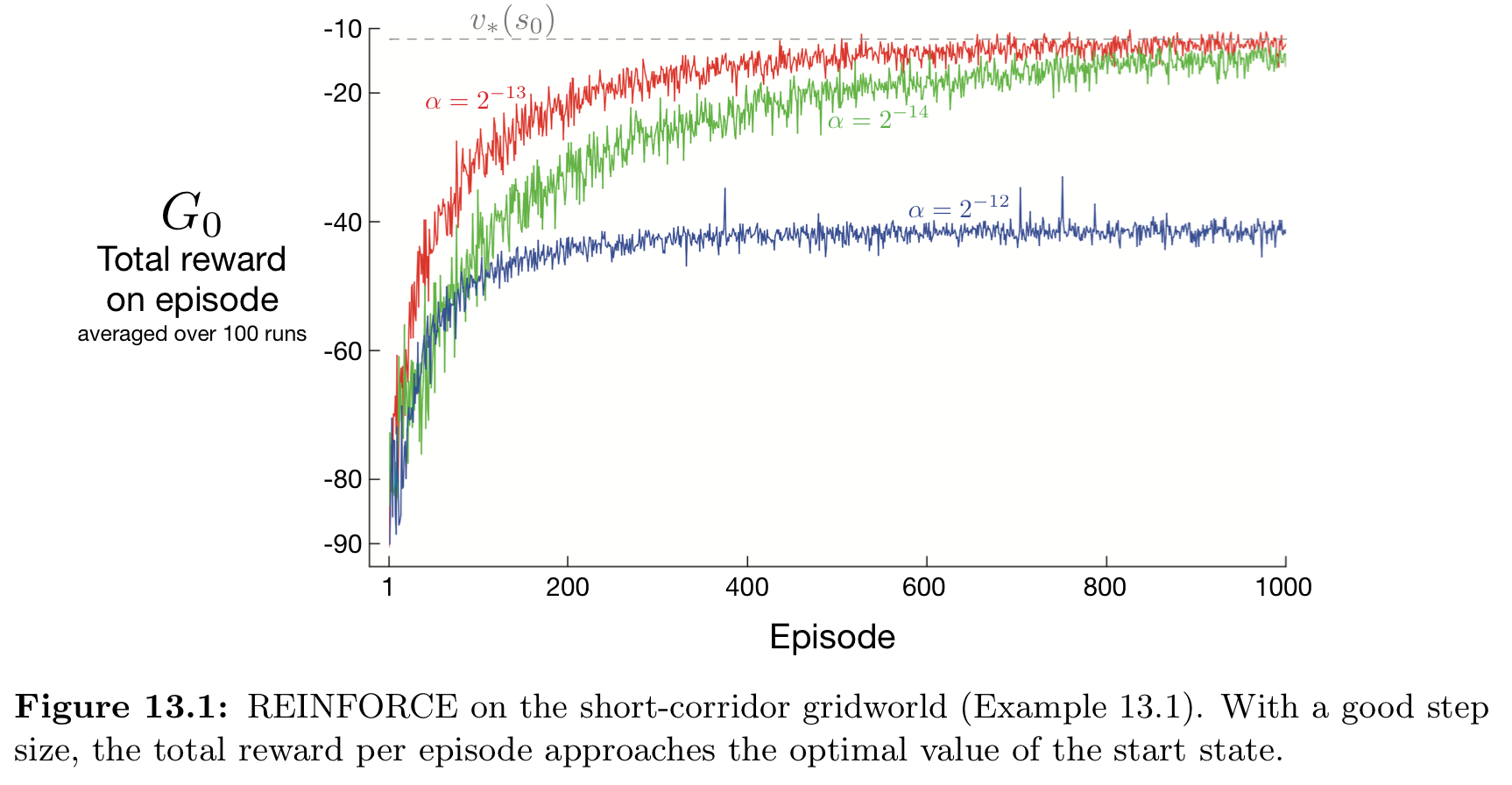：用的是标准的SGD，REINFORCE能保证converge，虽然可能high variance因此学起来慢。

13.4 REINFORCE with Baseline

(13.5) 可以加上一个baseline ：

[Intro to RL Chapter 13: Policy Gradient Methods] 相关文章推荐：

• 2023-11-24 11:00:14写好读书笔记对写作有哪些帮助
• 2023-11-09 01:01:18读书笔记的摘要和主要内容概述的区别
• 2023-10-30 19:00:44读书笔记对于阅读的重要性体现在哪里
• 2023-10-18 13:00:23用平板做读书笔记，推荐哪个软件
• 2023-09-20 11:00:39读书笔记就是摘抄句子吗
• 2023-08-29 17:01:33写读书笔记可以抄正在学的课文吗
• 2023-08-03 11:01:44你对读书笔记或者日记这种手写文字有怎样的认知 是不是和我一样有一种戒不掉的隐 你知道为什么么
• 2023-07-14 19:00:23如何写读书笔记，
• 2023-06-30 23:00:14如何教三年级学生学会写读书笔记
• 2023-06-29 12:01:30怎样引导孩子写读书笔记的感悟思考