欢迎访问喜蛋文章网
你的位置：首页 > 读后感 > 文章正文

Intro to RL Chapter 4: Dynamic Programming

时间: 2021-04-26 23:05:32 | 作者：斑马 | 来源: 喜蛋文章网 | 编辑: admin | 阅读: 101次

Intro to RL Chapter 4: Dynamic Programming

dynamic programming指已知MDP环境信息计算optimal policy的一系列算法。DP要求环境model，且需要大量计算，但它是理解其他算法的基础。DP的核心是利用value function来确定如何搜索policy。 v_*(s), q_*(s, a) 满足Bellman optimality equations，DP便是将Bellman equations转化为估计value function的算法。

4.1 Policy Evaluation (Prediction)

首先思考计算任意 pi 的value function v_pi ，称为policy evaluation in DP。 begin{align} v_pi (s) &= mathbb{E} _pi [R_{t+1} + gamma v_pi (S_{t+1}) | S_t = s] &= sum_a pi(a|s)sum_{s^prime, r}p(s^prime, r | s, a)[r+gamma v_pi (s^prime)] tag{4.4} end{align} gamma < 1 则value funtion存在且唯一。 考虑一系列 v_0, v_1, v_2, dots text{mapping }S text{ to } mathbb{R} ，随意选择 v_0 ，用(4.4)来估计下一个： begin{align} v_{k+1}(s) &= mathbb{E} _pi [R_{t+1} + gamma v_k (S_{t+1}) | S_t = s] &= sum_a pi(a|s)sum_{s^prime, r}p(s^prime, r | s, a)[r+gamma v_k (s^prime)] end{align} tag{4.5} v_k = v_pi is a fixed point for this update。当 krightarrowinfty ， {v_k} rightarrow v_pi 。这种方法称为iterative policy evaluation。有两种方法进行更新：一种维护两个array来存储state value；一种用一个array，有更新则立刻使用，会converge快一些。一般使用第二种。注意什么时候停止。

4.2 Policy Improvement

得到了一个policy的value function，就可以更新policy。首先考虑deterministic policy（本章中方法皆可扩展到stochastic policy）。考虑在一个state s 更新policy，选择action a ，若 q_pi (s, a) geq s_pi(s) ，即选择 a 后继续按照 pi 行动，得到的return大于 pi ，那么新的policy肯定比 pi 好， q_pi(s, pi^prime(s)) geq v_pi(s) 。同理推广到所有states， v_{pi^prime}(s) geq v_pi(s) text{, for all } s in S 。称为policy improvement theorem。当 v_{pi^prime} = v_pi ，满足Bellman optimality equation， v_{pi^prime} 必然是 v_*

4.3 Policy Iteration

不断做policy evaluation和policy improvement，每一步都可以得到strictly better policy，最终可以得到optimal policy。这种方法称为policy iteration这种方法的速度越来越快（猜的，因为value function的变化越来越小）。通常很快就收敛了。

4.4 Value Iteration

一个policy iteration的缺点是，每次都要policy evaluation。我们不必每次都等value function收敛，如value iteration： begin{align} v_{k+1} (s) &= max_a mathbb{E}[R_{t+1} + gamma v_k(s_{t+1}) | S_t = s, A_t = a] &= max_a sum_{s^prime, r} p(s^prime, r | s, a) [r+gamma v_k(s^prime)] end{align} tag{4.10} value iteration在同样情况下也保证收敛到 v_* 。另一种理解value iteration的方法是，它只是将Bellam optimality equation转化为update rule。同样注意什么时候停止：value iteration每一步包含一步policy evaluation，一步policy improvement。通常一步policy improvement + 几步policy evaluation会收敛更快。

4.5 Asynchronous Dynamic Programming

之前讨论的DP方法，都需要将state重复扫。asynchronous DP用任意顺序，利用任何available的下一步数据。有的数据可能更新几次了，有的可能还没更新，有的利用out-of-date数据更新。需要保证不忽略states，但很flexible。in-place iterative methods。比如有一种就是一次只更新一个state，逐个更新。只要保证所有的都能更新无限次就ok。不扫state并不意味着计算量减很多，只是通过选择state来加速，选择更新顺序来让信息流动更迅捷。有了asyn DP，我们也可以让agent和环境交互时，实时更新state value，让算法关注和agent关系更近的states。

4.6 Generalized Policy Iteration

policy iteration，value iteration，asyn DP都是policy evaluation和policy improvement的各种结合，最终目标都是找到optimal value function和optimal policy。generalized policy iteration (GPI) 来表示policy evaluation和policy improvement的交互。大部分RL方法都可以用GPI表示，即有不同的policy和value function，用value funtion来更新policy，让value function更接近policy的true value funtion。当evaluation和improvement都稳定时，即converge了，得到optimal，满足Bellman equation。policy稳定表示它greedy了当前value function；value function稳定表示它是policy的value function。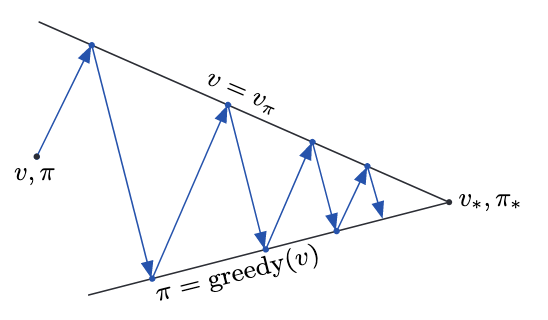evaluation和improvement既compete也cooperate。每一个更新都会让另一个unstabilize，但是同时都趋近于goal。有的情况下GPI可以converge，有的不行。

4.7 Efficiency of Dynamic Programming

DP可能不适用于大问题，但其实挺efficient。找到optimal的时间和states actions数成polynomial，而且还能保证找到optimal，比把所有policies都试一次好很多，which is exponential time。DP方法受限于curse of dimensionality，即state数量随着state variable的增长呈exponential growth。policy iteration和value iteration用得都很广泛，很难说哪个更好。一般都比worst case要好很多，尤其是initial policy，value设置得好。state很多时，一般用asyn DP。

4.8 Summary

用一个estimate来更新estimate，称为bootstrapping。在RL里很常见。
文章标题: Intro to RL Chapter 4: Dynamic Programming
文章地址: http://www.xdqxjxc.cn/duhougan/104315.html
文章标签：读书笔记
Top