星期二男孩问题与贝特朗悖论（概率论悖论收集：一）

前言：

最近复习概统，发现这门课程中著名和不著名的悖论尤其的多，于是打算收集一下.D

比方说，这是贝叶斯与全概率公式那一节中比较平凡的一个：检察官悖论，但它已经很令人头tom了：

图中的题目翻译：

'检察官悖论：

一位嫌疑人正在受审。

他的律师为他辩护：”如果没有更多的证据，这位嫌疑人只有百万分之一的概率有罪。“

不幸，控方律师又发现了一份新的证据，并表明：”如果嫌疑人无罪，这份证据只有0.001的概率被发现；但如果他有罪，这份证据则有0.999的概率被发现！“

求嫌疑人有罪的概率。

图中黑色字迹部分是我的作答，可以看到，反直觉的是，嫌疑人仍然只有 的概率有罪，这个悖论实际上跟今天所要重点讨论的两个悖论揭露的是同一个问题。

言归正传，今天要讲到的是星期二男孩问题与著名的贝特朗悖论（Bertrand paradox）。他们揭露了同一个问题，即：在定义概率时要事先明确指出样本空间是什么。

.........................................................................正文部分.................................................................................

星期二男孩问题：

首先，我们从这个问题的简单形式开始：

直觉上，许多人的反应都是1/2，但标准答案却是1/3。原因如下：

这个家庭两个孩子性别的所有可能组合为：{男男，男女，女男，女女}，但由于已经给定其中一个孩子是男孩，故不可能是{女女}这一种情况，即样本空间为：{男男，男女，女男}，一共包含三个元素，其中只有一种情况有两个男孩，故概率为1/3。

即该题是一个典型的条件概率问题，所求实际是P(有两个男孩｜有至少一个男孩），而直觉上的1/2实际描述的是P(第二个孩子是男孩)。

再看看星期二男孩问题本身：

'一个人有两个小孩，其中有一个是生于星期二的男孩，问另一个是男孩的概率是多少？'

逻辑是类似的，还是一个条件概率问题，即求P(两个男孩｜其中一个是星期二出生的男孩）。注意这里样本空间的划分要加上日期参数，即：{星期一男，星期一女，星期二男，...，星期日女}。

答案是13/27。这里用一段python代码穷举验算了一下：

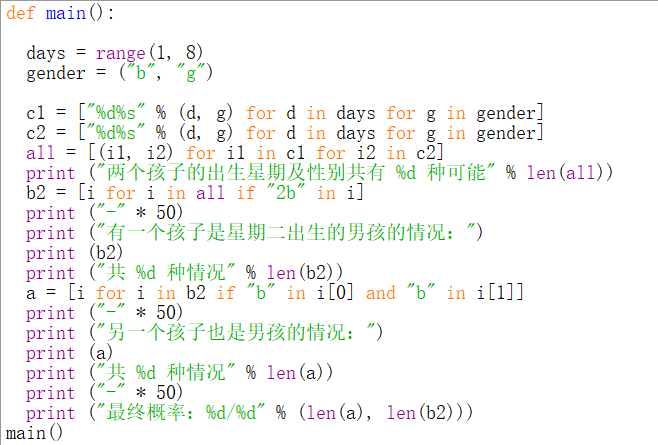
跑出来的结果：

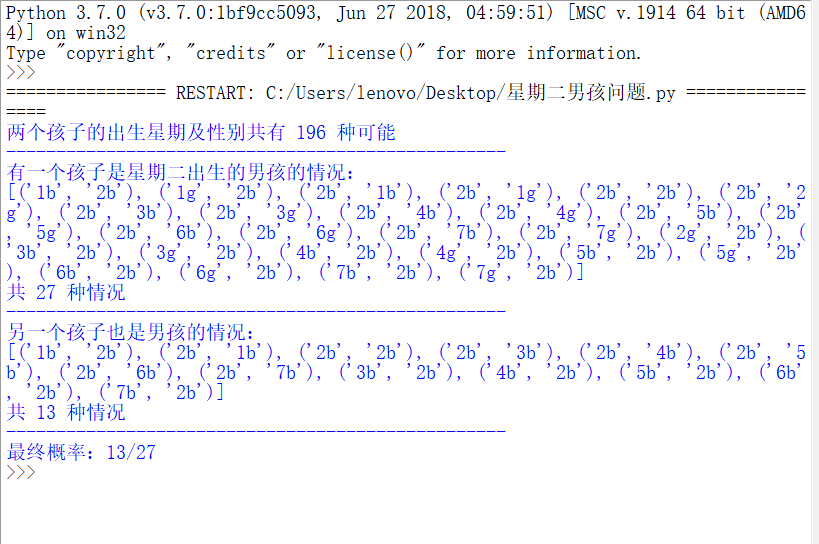
贝特朗悖论（Bertrand paradox）：

提到Bertrand paradox，要先介绍一下几何概率。

简单地说，几何概型需要满足两个条件才可以使用：无限性（连续，测度）和等可能性。

而贝特朗于1899年所提出的这个悖论直接指向了于19世纪末刚刚发展起来的几何概率的概念。

悖论内容是：

“在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形的边长的概率是多少？”

对此，贝特朗本人给出了三条结果不同的思路：

1). 由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3 。此时假定端点在圆周上均匀分布,圆周上的点组成样本空间S1。

2). 由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。此时假定弦的中心在直径上均匀分布，直径上的点组成样本空间S2。

3). 弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。此时假定弦的中点在大圆内均匀分布，大圆内的点组成样本空间S3。

显然，以上三条思路都是有效的，结果的不同实际上是由对于样本空间的不同选择引起的，而这三种不同的模型（样本空间）选择又是由于原命题中对于条件’均匀分布‘的限制存在歧义。

总结：

最后，其实以上三条悖论的本质都是相当平凡的。但是它们揭露了概率计算的过程中对于：所求内容，样本空间以及事件之间正确的逻辑关系进行严格定义的重要性。

概率计算 分析事件逻辑关系 应用、定义、性质 排列组合计算 结果

（完）

[星期二男孩问题与贝特朗悖论（概率论悖论收集：一）] 相关文章推荐：

• 2023-10-29 15:00:03关于帕金森手抖的科普知识
• 2023-10-11 01:01:09我怎样才能做好科普知识的博主
• 2023-04-24 14:00:12有关艾滋病的科普知识有哪些
• 2023-03-07 12:01:23有哪些有趣的飞机的科普知识
• 2023-01-31 09:01:41加强儿童、老人等重点人群新冠科普知识宣传，如何加强对重点人群健康的管理
• 2022-12-20 15:02:27大名鼎鼎的芝诺悖论该如何破解呢
• 2022-12-10 17:00:23有哪些关于太阳的科普知识
• 2022-12-01 14:01:21有哪些可以分享给朋友的关于动物的科普知识
• 2022-10-21 22:01:59你体验过用VR虚拟仿真技术学习应急安全科普知识吗
• 2022-10-18 18:02:05如何将一个难一点的科普知识传授给小学生