航天器的星下点轨迹

首先来介绍一下轨道要素，轨道要素又称为轨道根数，通过它们可以确定轨道平面在空间中的方位，轨道在轨道平面中的方位，轨道的形状和航天器在轨道上的位置，它共有6个，即轨道半长轴a，偏心率e，真近角 ，轨道倾角 ，升交点或降交点精度 ，近心点角距 。

星下点是指航天器与地心连线和地面的交点，星下点轨迹则是航天器的运动使星下点在地面形成的连续曲线。

如下图，将c点视为航天器在任意时刻的位置，那么星下点轨迹可以用下图来确定。

设地球在某时刻静止时星下点的位置为 ，那么根据 ， 和 就有：

就有：

同样利用几何关系可以有：

这样航天器星下点对应的经纬度就得到了。

但是地球在自转，因此 会变化，设 时刻（如入轨点或者某计算点）对应的升交点坐标为 ,其后任意时刻 的升交点经度为：

式中 为地球的自转角速度，大约15°/h,这样上面修正一下：

卫星连续两次通过升交点称为卫星运行一圈。

对于卫星轨道周期为T,地球自转会使升交点西移 。如果存在互质数A和B，那么360A = 15BN，即T = 24A/B。

A就是为实现星下点轨迹重复所需的最少圈数，B就是相应的恒星日数。

A= 1时,轨道就称为回归轨道， 时,星下点轨迹会在间隔A恒星日后重复,即为准回归轨道。

星下点附近一定宽度内的区域都是可观测区，即由航天器上观察地面的区域和地上可以观测航天器的地域。

从上面的公式可以看出,星下点轨迹可达到的南北半球的极限范围是纬度 等于航天器的轨道倾角 或 。

对于顺行轨道,航天器的星下点轨迹有时是从西南向东北,有时又是从西北向东南

对于逆行轨道则是为自东南向西北和自东北飞向西南的星下点轨迹。

如果航天器的角速度变化较大时,星下点轨迹(顺行轨道)的方向将不都是自西向东的走向了,局部会因为相对转速小于地球的自转速度,产生自东向西走向的星下点轨迹。

下图是在倾角为60 ,周期为3 h的圆轨道上运行的航天器的星下点轨迹，地球静止时为虚线：

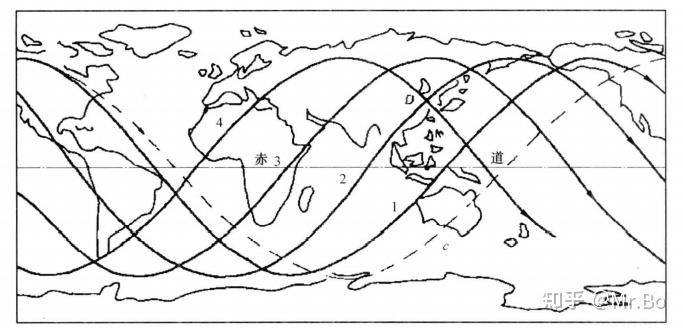
那么如果轨道倾角为零呢？

这样轨道平面将和赤道平面重合,此时如果轨道周期为24h(轨道高度35800km左右),则航天器环绕地球飞行的角速度将与地球自转角速度相同,其星下点会一直处于赤道上某处,相对地球静止。就是我们口中常说的同步卫星。

如果同步轨道倾角产生误差,为某一不为零的小角度,而其他参数准确时,则星下点轨迹变成下图，星下点每天以定轨点为中心南北振荡一次,振幅为倾角误差 ，走一个8字形轨迹：

[航天器的星下点轨迹] 相关文章推荐：

• 2023-11-19 09:00:09【眼健康科普课堂】眼睛痒，揉一揉就可以了吗
• 2023-11-18 17:01:05针对高压电缆护层接地环流在线监测，有什么科普的吗
• 2023-11-17 10:01:13【科普小知识】阴生植物为什么不怕照不到阳光
• 2023-11-16 12:00:38求科普，王自如是谁，是干啥的
• 2023-11-15 01:01:52在科研圈“立山头”的现象为啥感觉渐渐要进入“科普圈”
• 2023-11-08 11:00:16科普教育: 结核防治的方法是什么
• 2023-11-04 11:00:34在知乎上看紫微斗数算科普嘛
• 2023-11-03 08:00:27硬核科普 | 按钮开关的那些冷知识，你都知道吗
• 2023-10-30 08:00:43你见过最好的科普案例是什么
• 2023-10-30 08:00:04律师号怎么开启做 法律科普