浅谈聚类—从“距离”、“相似”到“社区”、“团体”，抽象术语中的现实意义

0x00 前言

忘了是出自哪里的一段话：

“世界上最遥远的距离不是生与死，而是我站在你面前，你却不知道我爱你。”

Taylor Swift的I Knew You Were Trouble里有一句词儿：

And he's long gone when he's next to me. And I realize the blame is on me.

对于距离和相似这一概念，不同视角的解读会带来不同的含义。我们通常可以说“学校到家的距离是999m”（随便编的），这是指物理世界中的远近概念，可以是两点直线上的距离远近，也可以是实际路程（存在弯曲路线）的距离远近；我们偶尔可能也会说“明明你就站在我面前，但我却感觉你很遥远。”，这里指的却是心与心的距离（抽象说法），虽然难以测度，但直观上来看不同的人之间确实有不同的亲近程度，也即具有差异化的“距离”，这种“距离”可能来自于兴趣爱好的差异、出身、教育背景的异同、性格上的契合与否等因素综合作用而形成，尽管抽象但不能不承认其存在。类似地，我们也可以认为不同的言语之间具有不一样的“距离”，如“我爱你”、“我喜欢你”、“今天会下雨”三句话之中直觉上感知前两句话要比后两句话相似/距离更小（如果您认为后两句更相似，我觉得会是很有意思的观点，欢迎讨论）。由于“相似”可看作是“距离”的对立，所以对于“相似”的解读也可以有多种视角。

既然“距离”和“相似”具有那么多解读，那么类似“物以类聚，人以群分”的话语要怎么理解？什么样才叫“类”、“群”？按照百度百科的说法：

「物以类聚，人以群分」：类：同一类。 同类的东西聚在一起，人按照其品行、爱好而形成团体。指好人总跟好人结成朋友，坏人总跟坏人聚在一起。

品行、爱好相似的人可以形成一个团体，就类似大学里的社团，有一些人因为共同爱好摄影而组成了摄影社，有一些人组成了足球社、日语社等等。总之是人的某些相似的属性或者是相互吸引的因素促成了团体的形成。当然，人们也不一定只有单一的爱好或属性且随着时间的推移，爱好和属性都可能发生变化，所以一个人在同一时间段内可以属于多个团体（如在多个兴趣社团、打上多重性格的标签等），且过一段时间后或许会因为发生了极大的转变而大大地改变了其社团活动的类型，相比较而言，不具有生命的物体「或许」变化还少些。

注：如无特殊说明，本文的「团体」、「社区」、「类簇」具有相同的含义，都是指某些（不知因何因素而）联系紧密的人或物组成的一个人或物的集合

所以，给人打标签是很有挑战的问题，你要给他打多少个标签才合适？（哪些标签最能够概括这个人？）；什么时候应该对一个人刮目相看？（打完标签之后人还是在变换的，标签的现势性如何？）；要想准确滴把握一个人的特性，需要考虑什么因素？

上面所提的一些问题很直观，其中一些准则也指导了“数据聚类”或“社区分割”方法的发展。

但是有时候我们可能也会纠结：同一类的事物一定要“相似”吗，他们可否是不相似但却因为某种原因而经常在一起出现？或者说我们在进行聚类或社区划分时要不要考虑这种情况？

陈奕迅的新歌《是但求其爱》中有一句词儿：

纵双方理念多相同 却不相融 莫论陪衬

其中蕴涵了某种现象：在一起玩得很嗨的朋友或配偶不一定很相似，而可能是对方具有的自己所不具备某些特征吸引了双方的交互，三观相似的人也不一定就能走到一起。当然这句话本身过于空泛可能仔细读来没什么意义，毕竟驱动两个人或一伙人聚在一起的原因有太多太多：有的可能是由共同的目标、利益驱动（类似梁山一百零八好汉，红花会群雄）；有的可能是因为性情相近意气相投而聚首（胡一刀夫妇）；有的却可能是彼此填补了对方的某种空白（如陈家洛和香香公主，香香公主“世间一死宁无惧？君为家山我为君”）……

总结起来：表面的特征相近不一定使得人聚在一块儿；内在特征相近的人相见可能会有意气相投相见恨晚的念头。那问题来了：

表面、内在特征那么多，哪些特征更能作为判断一伙人会否算“一类人”？

【PS：谈男女朋友不一定双方很相似，首先身体特征、性别特征等表面特征肯定是不相近的，很多成功伟大的爱情，男女双方在性格、能力方面其实是互补的，这样可以说两个人组成了一个“类”吗？“类”内元素真的要有相似这一条件作为保证吗？或者说“相似”到底该限定在什么范围内讨论才合适？“一类人”跟“一路人”有分别吗？】

还有很多可以细细argue的实际问题：

曹操、刘备、孙权三人虽性格才情不一，但各是一方领袖，算是“一类人”吗？关羽有一段时间“降”了曹操，那段时间里可以认为关羽这种“身在曹营心在汉”的人是曹操阵营的吗？……

总而言之，除非作了很具体的概念限定，否则三言两语似乎也很难说清楚“一类人”到底是如何划分的。这也是工程落地时很注重特征工程的原因，针对某一具体的业务场景、业务目标选取能够更合适的一些特征作为类别划分的依据，而非把特征一股脑儿地放在一块，然后调用一个算法去“聚类”，要考虑现实的需求。本文接下来的章节将先分普通数据、图数据介绍一些框架性的聚类、社区划分算法，然后介绍现有的多样性的“距离”、“相似度”的概念定义，最后总结在什么场景下更适合使用什么方法，也希望众多经验丰富或有独到见解的前辈能够指出本文的不足或对本文遗漏作出补充。

0x01 经典聚类算法串讲

本章节假定读者具备一定的机器学习、网络科学、图论的常识，知道聚类是要对数据点（表示某个实体，可以是人、物）根据其特征按照一定的规则进行自动化的类别划分；社区划分其实也是聚类的一个分支，只不过面向的是组织结构为图的数据，划分出的“类别”往往是由联系紧密的节点组成，本质上是我们除了知道数据点（实体）自身的特征之外，还知道实体之间「一定」的关系/联系，希望在具备这些信息的情况下进行类别的自动划分。设计这些自动化类别划分方法对于现实场景下的应用而言是有好处的，最容易想到的就是辅助人来进行类别划分、减少人的工作量（比如对图书馆的馆藏书籍进行自动打标签，预先把特征相近的书籍分在一起；在风控系统中识别金融诈骗团体；……），在如今大数据爆炸的场景下这种辅助手段是更加有必要的。

1. 常见的聚类方法

上过机器学习基础课的同学大概都听过KMeans、DBSCAN、谱聚类等聚类方法。如果用过sklearn等机器学习工具包还会发现有一些聚类方法叫BIRTH、OPTICS、Gaussian Mixture等方法。多种多样的聚类方法中实质上都是对如下问题的具体化：如何定义类簇？如何获取类簇？做出不同的具体化来源于实际需求，如依据现实中数据的分布特征来定义“合理”或“合适”的类簇。事实上，当你能够定义类簇，或者描绘出类簇应有的特征，设计获取类簇的方法就比较简单了。

比如说KMeans算法，它将类簇定义为样本点的平均值。获取类簇的流程为：先假定样本数据集中包含k个类簇，因此先随机初始化k个点作为不同的类簇中心 ，然后将距离类别c最近的点划分到这一类别，重新计算类簇中心，迭代地进行类别划分，类簇中心计算直到收敛就得到类簇结果了。KMeans算法蕴含的思想就是通过距离来划分类簇，其实就是老话说的“近朱者赤，近墨者黑”，如果样本点距离类簇A的中心点比较近，就认为样本点属于A类；如果距离类簇B的中心点比较近则认为样本点属于B类。通过不断迭代最后收敛得到的划分结果就是聚类结果。流程如下图所示：

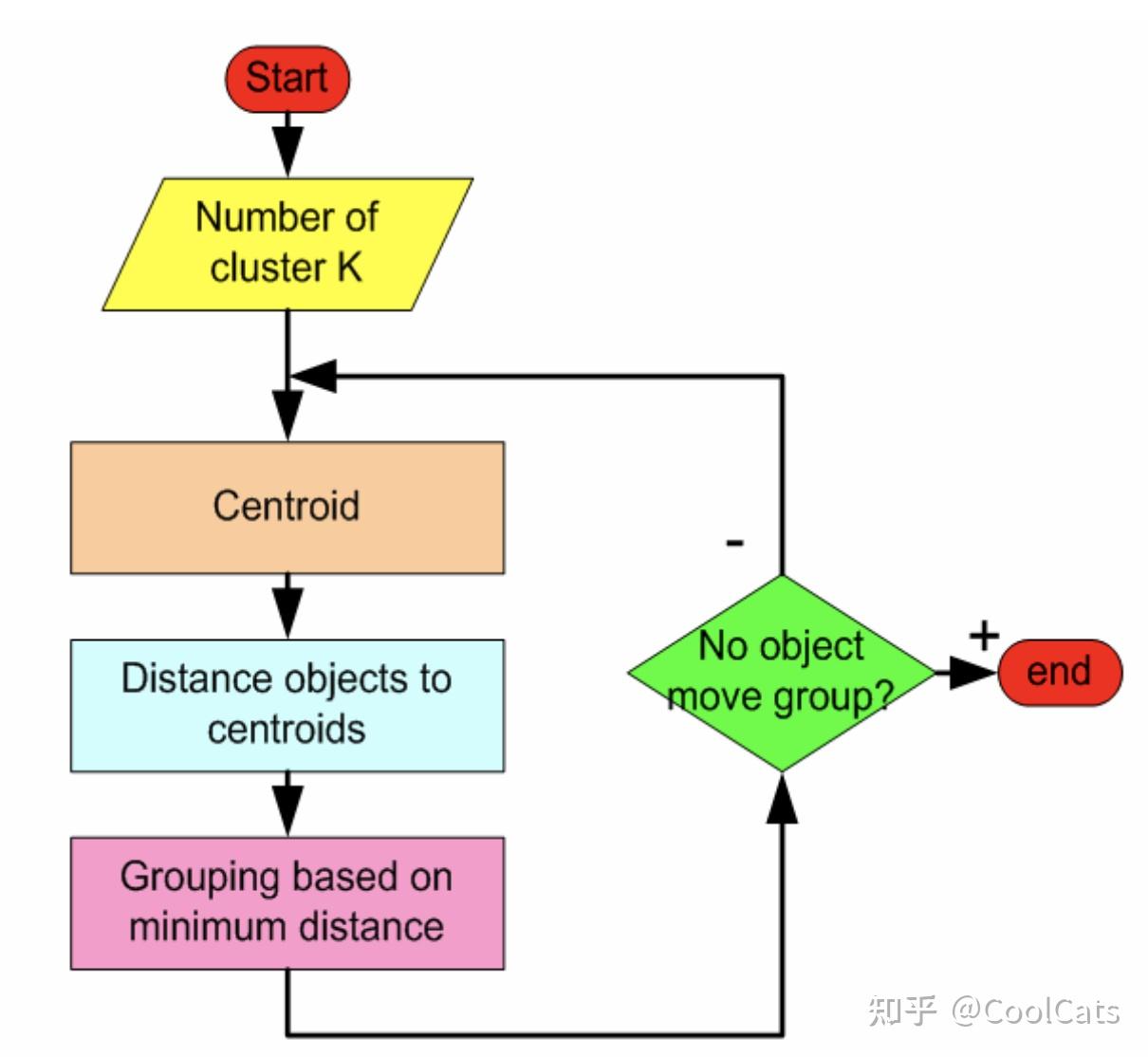
在斯坦福大学提供了一个在线KMeans可视化的网站，读者可以参考获得对该算法更直观的体会。Visualizing K-Means Clustering

当然，有同学会问为什么KMeans算法一定会收敛？如何选择类簇的个数k？该算法得到的聚类结果真的是合理的聚类结果吗？聚类结果是否唯一确定？这确实是很重要的问题，但这里先把这些问题放一放，后面再详加解释。等不及的可以先参考：Download K Means Clustering Tutorial

再举几个例子，比如说DBSCAN聚类，这个算法用一种与KMeans不同的角度——密度——来理解类簇，因而也就有了不同的获取类簇的方法。我们先看下面的图，然后想想从自己的直觉出发比较合理的聚类结果是什么样的？

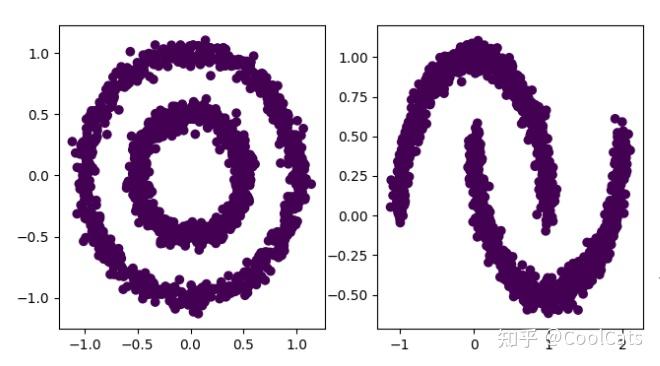
相信大多数人都会觉得两个数据集的合理聚类数均为2个，左图所示数据的合理的聚类结果是内圆环、外圆环；右图所示数据的合理聚类结果为两个月亮，如下图所示：

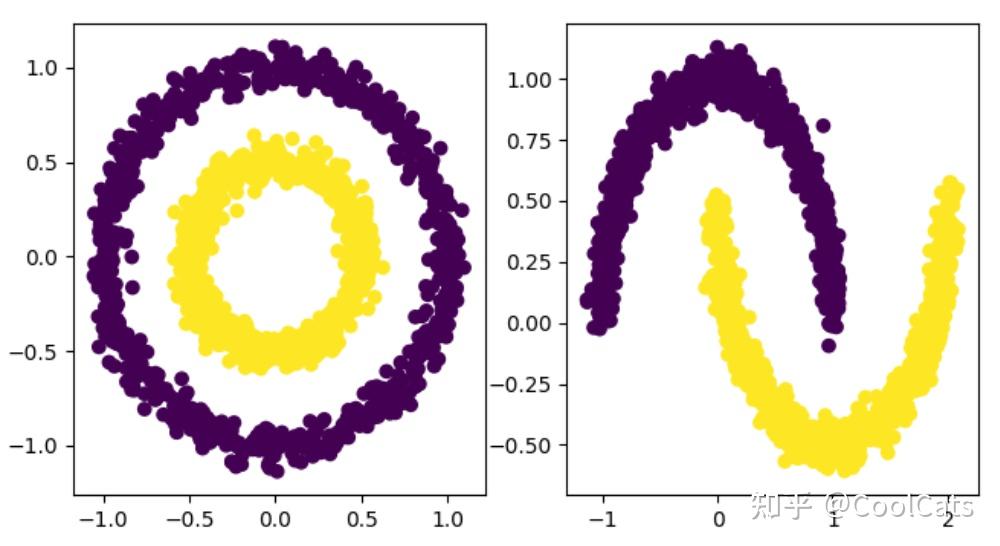
不难理解，通过上面所介绍的KMeans算法是无法获取上图所示的聚类结果的，其仅仅按照距离最近来分配类簇会导致一些从宏观上看属于一个整体的对象被割裂，也就是说KMeans算法具有“不能处理任意形状的类簇”的缺点。而DBSCAN的思路是：将类簇定义为空间中具有分布密度足够高的样本组成的最大集合。这里的关键就是“密度”和“足够高”。怎么计算样本空间中某一区域的样本密度？密度超过什么范围认为是“高密度”，样本点形成了一个类簇？

所以DBSCAN算法就会有两个参数：

：邻域的大小，表示每个样本点的“辐射范围”，如果两个样本点的距离在 范围内，则认为这两个样本点是一伙的（属于同一个类簇）。所以，这个参数实际上用来回答：空间中的两个点要离得多近才认为他们属于同一个类簇？

minPoints: 参数从微观的角度定义了两个样本点属于同一个类簇所需要满足的一个必要条件，但两个样本点不一定足够形成一个类簇，我们是分布密度要“足够高”才称其为一个类簇。当然我们也可以认为两个样本点能够组成一个类簇，此时minPoints=2，如果认为至少要5个样本点才能组成一个类簇，则minPoints=5。也就是说minPoints定义了一个类簇最少需要包含多少个样本点。也因为有此参数，存在一些样本点不会被划分到任何类簇中，此时我们认为这些样本点为噪声。

从对DBSCAN参数的介绍可以知道，DBSCAN不需要提前指定类簇数量，其通过样本点“拉帮结派”和“扩张”的方式定义类簇，因此有潜力在任意形状的数据集中发现类簇。

用通俗的语言来粗略形容DBSCAN就是：社会上有形形色色的人，有一些志趣相同而且相距比较近的人先形成了帮会（类簇），然后帮会通过里面成员的人际关系进行扩张，扩张到人际关系的极限为止。这样就形成了很多个帮会，同时也会有一些不在任何帮会中的离群的人（或许是不喜社交，或许是被排斥，总之与其他人保持一定的距离，缺少交集）。

但是DBSCAN也有一些缺点，如其在参数设置时使用了全局的参数，这可能导致算法在“不同类簇密度差距较大”的情况下失效（如忽略了局部密度很大但从全局角度来看密度相对较小的一些类簇，或将局部密度极高的点与周边密度明显较小的点集合并为一个类簇），对于这类问题也有一些方案，如在DBSCAN的基础上做了改进的OPTICS算法，读者可以自行参考。

我们来进一步拓展，前面所介绍的KMeans和DBSCAN有一些共同点，如都是基于“划分”的算法，其通过某种规则将点划分到某一个类簇中，具体来说，KMeans通过距离划分，DBSCAN通过从核心点密度可达这一条件来进行类簇划分。这种将每个对象分配到一个类簇中的聚类方法称为划分型的聚类算法。但很多场合下对象的真实类簇结构可能并非是对样本进行一次划分就能够客观描述的，真实类簇结构可能是层次的，比如从宏观的角度讲，家猫和老虎都是属于猫科动物，但细分来看，老虎这一类动物也可以分东北虎、西伯利亚虎、华南虎等亚种类别；再比如，DBSCAN、OPTICS、KMeans都是划分型的算法，但再细分的话DBSCAN、OPTICS属于基于密度的聚类算法，而KMeans属于基于原型的聚类算法。前面介绍的划分型算法无法获得层次性的类簇结构，于是我们便有了层次聚类方法。

层次聚类的基本思路是：首先将样本空间中的所有对象看作同一类别，然后自顶向下地按照一定的准则进行类簇的分解，这又称为分裂式层次聚类；或者先认为每一个对象各自属于一个类别，然后自底向上地按一定准则进行类簇合并，这称为凝聚式层次聚类；如此可以得到在多个层次上的类簇划分。那么按照什么原则进行类簇的分解或合并呢？这里又可以借鉴划分型算法中的思路如按照距离最近原则进行类簇合并，按照距离最远原则进行类簇拆分。

层次聚类算法有：AGNES、DIANA、WARD等等，这里就暂时不介绍了。

这里我们简单回想一下上面所介绍的方法，比如KMeans，每次聚类的时候只为对象分配一个类别，但是现实生活中，我们对于某个对象可能无法做出确切唯一的类别界定，模糊性和不确定性在现实生活中更为常见。导致模糊和不确定的原因主要是信息的缺失，比如我们分析用户消费数据时，仅根据现有的用户资料和消费记录我们可能很难判断这个用户是王菲的歌迷还是周杰伦的歌迷或是两者的歌迷。在聚类领域中，根据方法“是否将数据确切地分到某一类中”可将方法分为硬聚类和软聚类两类，前者将数据点确切地分到某一类，如KMeans、DBSCAN；后者将数据按一定概率分配到某类中，如高斯混合模型、模糊c均值聚类。在现实大多数应用场景中，软聚类或许是更需要的方法，比如在地理空间分析中，许多地理要素具有模糊性，一块城市区域既属于商业区又属于重要交通枢纽；一个山头既属于林区又属于高海拔区域，这些都是我们在进行聚类之前需要考虑清楚的。

除了上面说的聚类方法，还有一些从非常独特的看待类簇的角度，如谱聚类的方式从一个更为抽象（当然，如果你了解或学习过谱图理论，或许不觉得抽象）的谱视角来看待对象之间的联系，通过图分割的思路来进行类簇的划分。还有量子聚类、核聚类等高大上的方法，总之，每一种方法都代表着一种看待“类”的视角。

2. 网络社区划分方法（暂略）

Newman、K-Clique、Infomap

0x02 关于“距离”和“相似度”

前面介绍了几个经典的聚类方法，并对方法进行了一定的分类。这一章梳理一下经典的“距离”。在聚类里面，可以说最为重要的一部分就是对“距离”的理解，这实际上与“什么是类”这一问题息息相关。在KMeans里面我们按照距离类簇中心的远近来为样本点重新分配类簇，DBSCAN会根据距离大小决定是否一个点能从核心点密度可达。但到底什么是距离？对于某个任务来说什么样的距离度量是合适的？

最基本的要求就是满足距离的条件：非负性；对称性；传递性。

在基本要求达成后，还需要与分析对象的物理意义保持一致，这就要具体情况具体分析，关键就是说得过去。比如你要度量两个同学对课本掌握程度的差距（距离），可以用他们学习成绩的差值作为度量，但用身高的差值来度量就不合适了。

欧式距离

这是很直观的距离概念，从小学开始就已经接触了，在二维或三维的世界中，我们通常（注意，是通常）使用欧式距离计算两个点的距离。

欧式距离具有的局限性：认为每一个维度都同等重要，不能考虑不同维度间的相关性。（马氏距离弥补了这个缺漏。）

曼哈顿距离

地理空间中两个点之间往往存在很多障碍物或者拓扑约束导致从一个点到另一个点的实际路线不是直线，而是曲线，所以说在城市空间点的距离度量中，欧式距离可能是不适用的。如下图所示的在网格状的城市街道空间中，车子从一个点到另一个点往往不能直线到达，只能沿着街道曲折前进，此时欧式距离不能反映两个点的真实行程距离，真实的行程距离就是曼哈顿距离。当然，如果是更复杂的拓扑邻接关系（如两个点之前虽然有路，但其中路段却是单行道），则需要再做扩展。

余弦相似度

两个向量夹角的余弦值可以作为两个向量的方向相似度度量，余弦距离就可以定义为1-余弦相似度。吴军博士的《数学之美》一书中对余弦相似度有一个专题的科普介绍，或许你想不到看似简单的余弦相似度居然是谷歌新闻自动分类的一个核心技术。

与欧式距离相比，余弦距离更关注方向上的差异，而不关心数值上的绝对差异。

举个例子，比如A同学一年打10小时羽毛球，200小时篮球；B同学打100小时羽毛球，1999小时篮球；C同学打1000小时羽毛球，200小时篮球。虽然A同学和C同学一年都打200小时篮球，但C同学打羽毛球的时间明显多于打篮球的时间，A同学打篮球的时间明显对于打羽毛球的时间，我们更可能会说C同学是羽毛球爱好者，A同学是篮球爱好者，同理B同学是篮球爱好者，虽然A和B打篮球的时间从绝对数值上有较大差距，但横向对比不同的运动项目，A、B同学都是更偏好篮球的，通过余弦距离来度量的话A、B之间的距离是比A、C距离小的，所以这个案例中要做运动偏好聚类分析的话使用余弦距离度量比欧式距离要合适。但如果是做运动强度（时间）聚类分析的话，欧式距离就更合适了，因为这里强调的是绝对数值上的差异。

共享最近邻距离

在社交网络里，我们考虑两个用户是否相似，不会通过他们拥有好友的数量来判断，而更可能通过他们共同好友的数量来判断，大家可能会注意到QQ中会有“你可能认识的人”这一功能，然后会看到在推荐列表最前的用户与你具有最多的共同好友，这里就蕴含了共享最近邻这一思想。有学者利用这个思想提出了共享最近邻聚类方法。

马氏距离（Mahalanobis Distance）

前面提到欧式距离会将特征的每一个维度同等对待，而实际上不同维度的特征可能贡献不同，在特征空间中，某些维度之间可能具有较强的相关性。马氏距离为这一问题提供了一个解决思路。其通过协方差矩阵考虑了变量之间的相关性，可以查看Ph0en1x写的知乎文章。

推土机距离（Wasserstein 距离）

推土机距离度量了从一个概率分布改变到另一个分布所消耗的最低成本/代价，具体可参考文章。

文档距离

自然语言处理里面的一个常见分析对象就是文档，如何度量文档之间的距离？直觉上来看通过欧式距离或者曼哈顿距离都不合适。曾经余弦距离是比较流行的文档距离的具体形式，后来有研究者提出WMD（Word Mover Distance）距离，其在使用词嵌入向量作为单词、句子表示的基础上引入最优传输距离，定义了WMD距离，即这里所指的文档距离，其对于文档分类、聚类有较好的表现。

DTW距离

我们的研究对象不只点、文本，还可能有时间序列，语音识别领域通常需要度量两段语音之间的相似度，量化金融领域需要度量两只股票走势的相似度，这时上面介绍的距离就都失效了，但此时还有DTW距离！

DTW距离的局限性在于要求两段时间序列具有相同的长度，虽然我们可以通过裁剪等预处理手段达成这个要求，但始终不是很方便；而且在DTW框架下，个别具有较大差异的点会对最终的距离度量产生较大影响，这可能不是我们想要的。

最长公共子序列（LCSS）

对于个别差异很大，但大多数情况下形态相似的两个序列，可以使用LCSS作为距离度量。LCSS在轨迹聚类、分类中有广泛应用。

0x03 未来计划

有时间对各类或者单个算法的来龙去脉、优化方案、评价方法进行专题总结。

参考资料

2.3. Clustering - scikit-learn 0.24.1 documentation​scikit-learn.orgpeople.revoledu.com​people.revoledu.com

people.revoledu.com

people.revoledu.com​people.revoledu.comhttps://towardsdatascience.com/how-dbscan-works-and-why-should-i-use-it-443b4a191c80​towardsdatascience.com

Self-Supervised Learning in 2021: In-depth Guide

https://towardsdatascience.com/how-dbscan-works-and-why-should-i-use-it-443b4a191c80​towardsdatascience.comSelf-Supervised Learning in 2021: In-depth Guide​research.aimultiple.comhttps://scholarsmine.mst.edu/cgi/viewcontent.cgi?article=1763&context=ele_comeng_facwork​scholarsmine.mst.edu

KMeans初始化：Download Limit ExceededKMeans初始化：

Download Limit Exceeded​citeseerx.ist.psu.edu

距离度量

https://www.researchgate.net/profile/Lior-Rokach/publication/226748490_Clustering_Methods/links/02e7e536dcb9b70ea3000000/Clustering-Methods.pdf​www.researchgate.net

可视化聚类

Visualizing K-Means Clustering​www.naftaliharris.comVisualizing DBSCAN Clustering​www.naftaliharris.com

[浅谈聚类—从“距离”、“相似”到“社区”、“团体”，抽象术语中的现实意义] 相关文章推荐：

• 2022-11-15 14:00:09普通人全面深入了解人工智能（机器学习，深度学习，强化学习）的路径，可以如何描绘
• 2021-04-12 08:51:14通俗解释什么是机器学习