[10]三力汇交推导看横幅最佳视角

我交终于开学了，我骑车疾驰在学校梧桐西道上，仰头发现前方有一个写有鼓励垃圾分类的横幅，我在受到道德光芒洗礼的同时，发现一个有趣的现象：

离远了吧，就会看不清条幅上的字，离太近依旧效果不好。如下图：

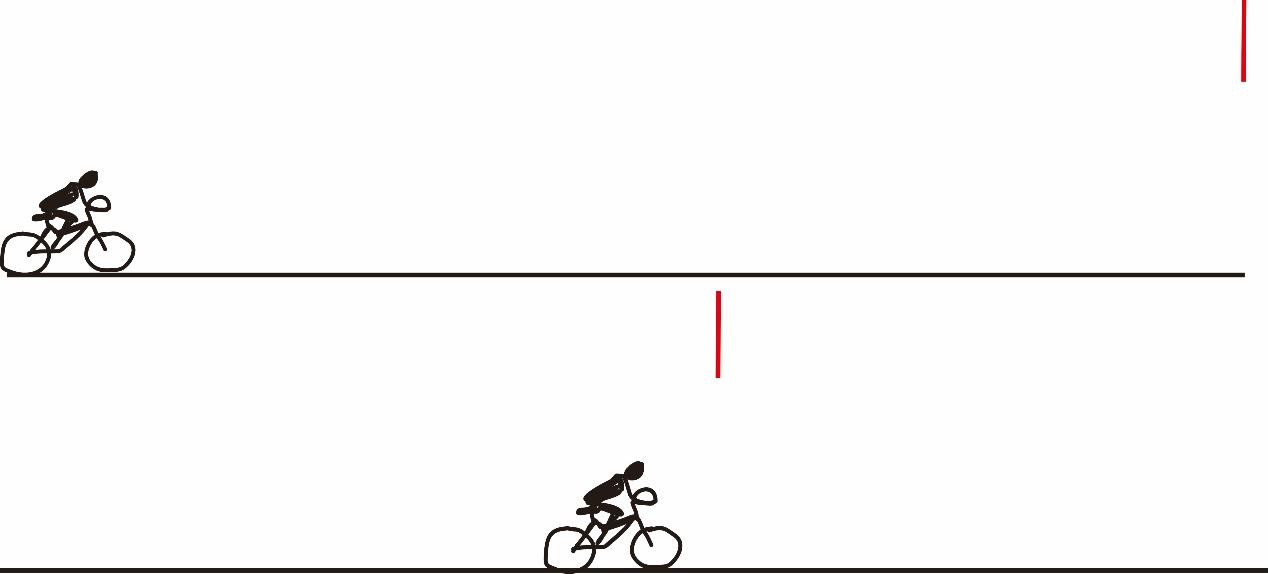
究其原因，我发现两者看不清都是视角过小的缘故，如图：

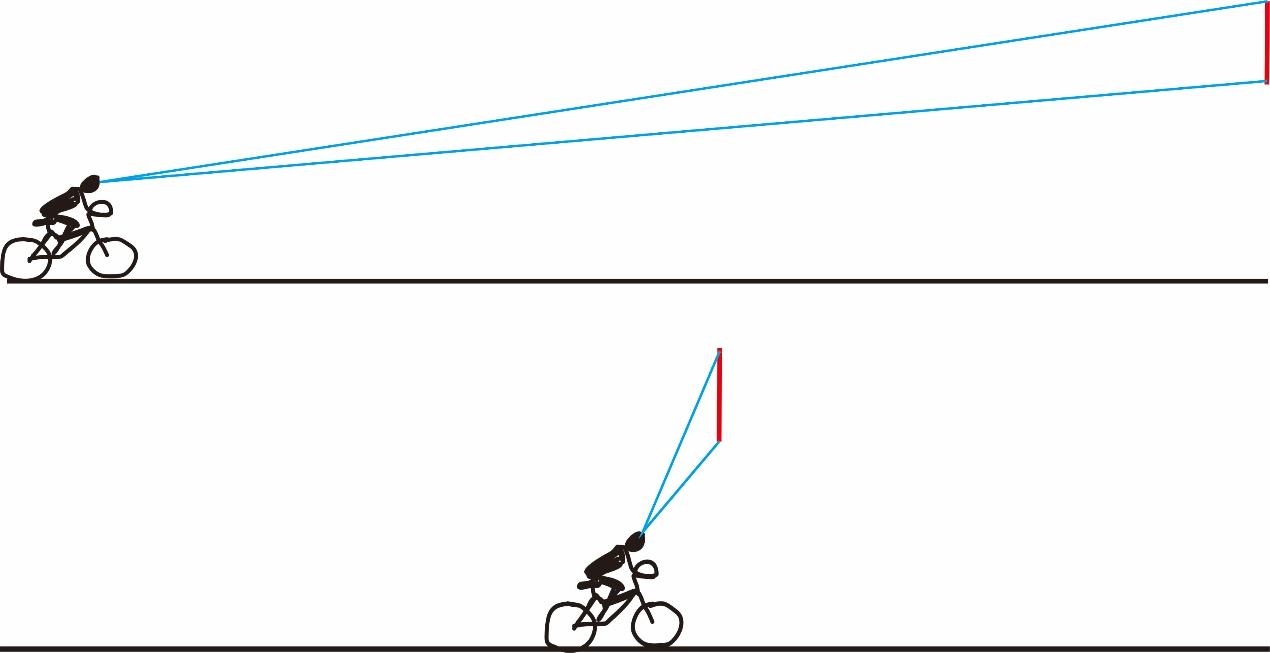
我自然想到：既然过远和过近都会视角过小，那么一定存在一个位置取到最佳视角。如何求该点位置呢？

假设：1.因为我刚换眼镜，不考虑因视力问题影响观看效果，即不考虑距离，仅考虑视角

2.假定我骑车时眼睛高度不变，但是可以抬头，且横幅高度不变（很合理）

3.不考虑主观上人眼最舒适视角，简单认为角度越大，效果越好

先说结论：

与横幅距离为其上下高度的几何平均数时，取得最佳视角。

当然这个你设出变量，再求导出最值一定能够做出来，但依照本专栏的惯例，依旧采用物理方法解决

构造模型如下：

为光滑直杆，套有小环（代表眼睛位置），刚性轻杆 与小环焊接（代表视线），两杆之间有原长为零的弹簧， 处与光滑套筒连接。

推导如下：

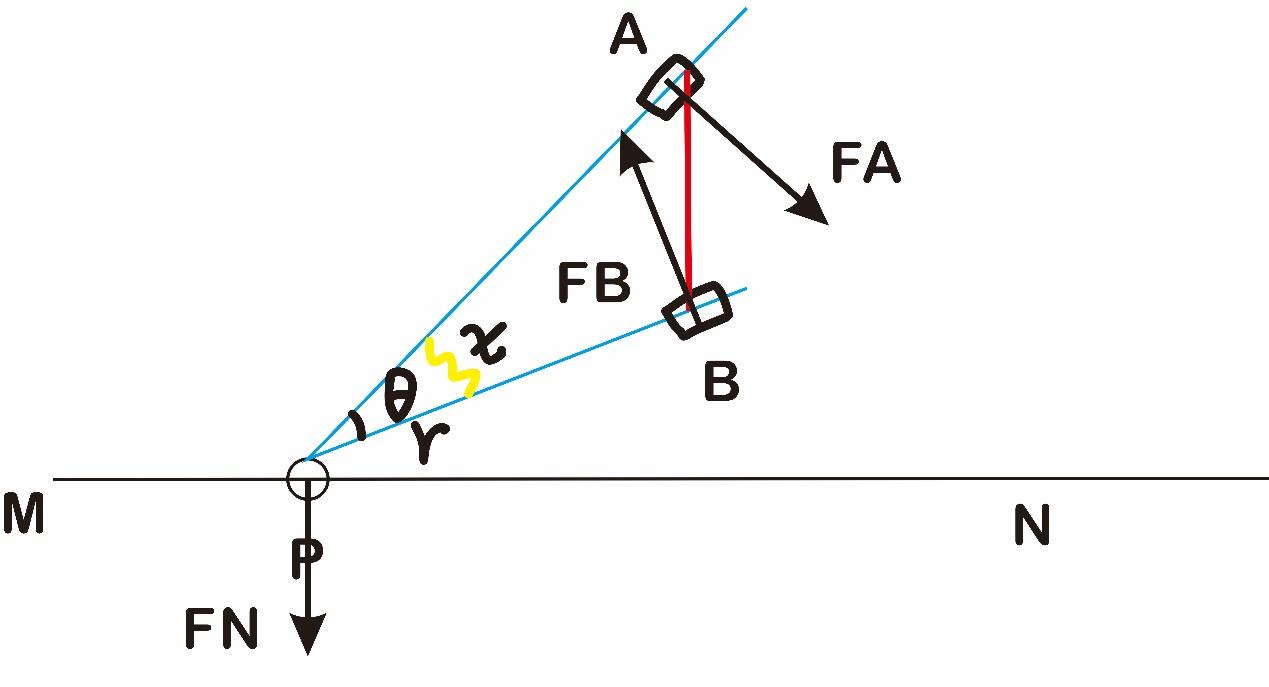
视角 最大时 最大，弹簧势能取极值，此时受力平衡

以 整体为对象

因为套筒光滑，故 垂直于杆，

因为 光滑，故 垂直于 ，

弹簧弹力是系统内力，不考虑，

对象只受三个力，由三力汇交，得视角最大时如图：( 为汇交点)

既然都看出圆了，直接几何关系：

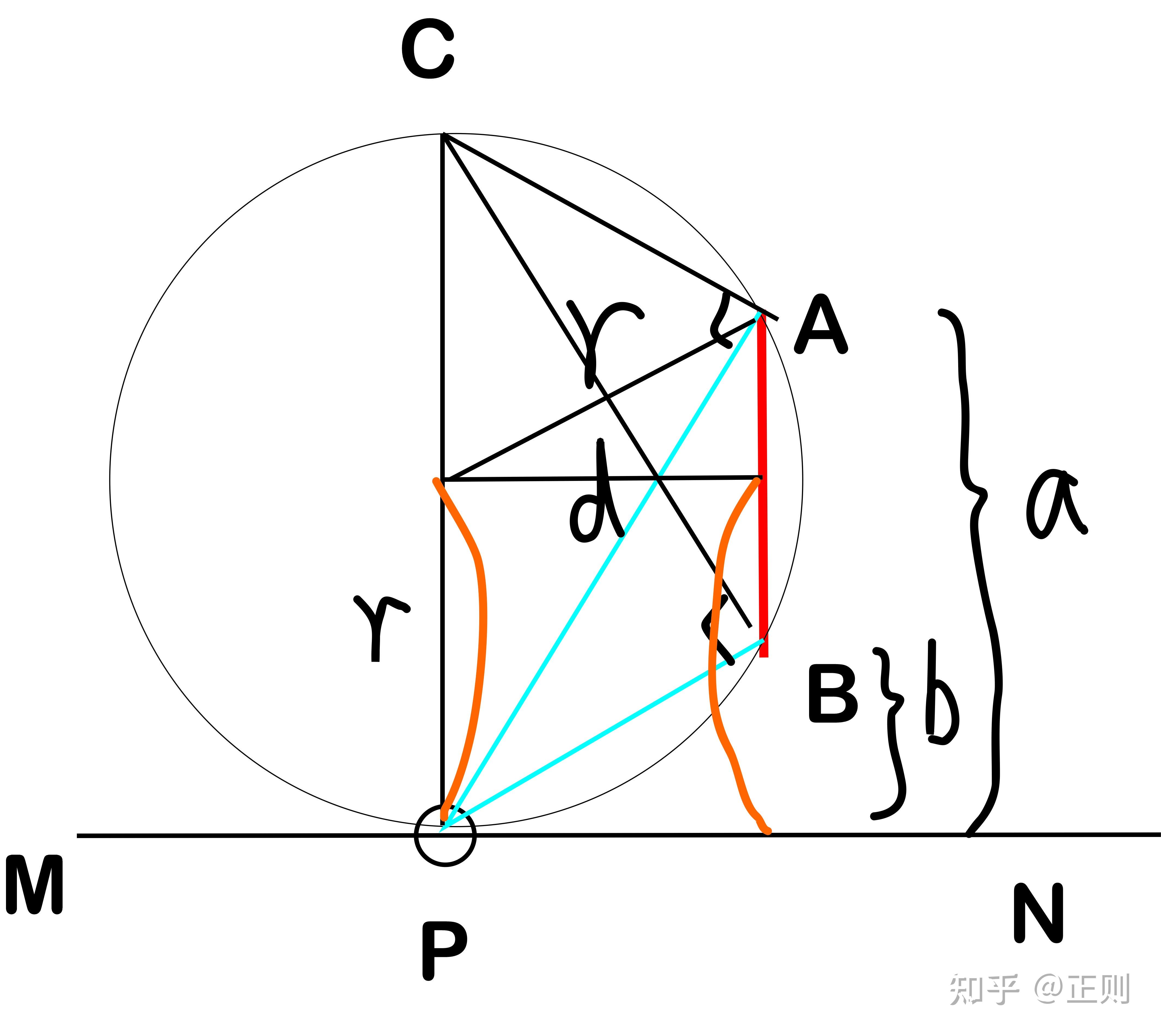
由勾股定理，

由图中橙色边长相等，

联立得

即：与横幅距离为其上下边高度的几何平均数时，取得最佳视角。（取眼睛高度为基准）

因时间原因，笔者会不定期更新，欢迎关注此专栏，以便最快获得更新信息哦。

[[10]三力汇交推导看横幅最佳视角] 相关文章推荐：

• 2023-03-13 09:04:56物理科普的渠道有哪些
• 2023-01-02 12:04:32理论物理科普有什么意义
• 2022-10-26 21:00:18高二 有哪些关于物理科普类的书啊
• 2022-01-02 03:00:56有哪些好的适合高中和大学的物理科普书籍